Khan Academy on a Stick
Introduction to algebra
Videos exploring why algebra was developed and how it helps us explain our world.
-
 Origins of algebra
Origins of algebra
Where did the word "Algebra" and its underlying ideas come from?
-
 Abstract-ness
Abstract-ness
The general idea behind the word 'abstract'
-
 The beauty of algebra
The beauty of algebra
Why the abstraction of mathematics is so fundamental
-
 Descartes and Cartesian coordinates
Descartes and Cartesian coordinates
Bridging algebra and geometry. What makes linear equations so linear.
-
 Why all the letters in algebra?
Why all the letters in algebra?
Jesse Roe and Sal Khan talk about why we use letters in algebra
Overview and history of algebra
Did you realize that the word "algebra" comes from Arabic (just like "algorithm" and "al jazeera" and "Aladdin")? And what is so great about algebra anyway? This tutorial doesn't explore algebra so much as it introduces the history and ideas that underpin it.
-
 What is a variable?
What is a variable?
Our focus here is understanding that a variable is just a symbol that can represent different values in an expression. We got this. Just watch.
-
 Why aren't we using the multiplication sign?
Why aren't we using the multiplication sign?
Great question. In algebra, we do indeed avoid using the multiplication sign. We'll explain it for you here.
-
 Evaluating an expression example
Evaluating an expression example
Evaluate the given expression where the variable could have 3 possible values. Understanding how expressions are interpreted according to different variable values is a huge new skill. Pat on the back!
-
 Evaluating an expression using substitution
Evaluating an expression using substitution
In this example we have a formula for converting Celsius temperature to Fahrenheit. Let's substitute the variable with a value (Celsius temp) to get the degrees in Fahrenheit. Great problem to practice with us!
-
 Evaluating exponential expressions 2
Evaluating exponential expressions 2
Evaluating exponential expressions 2
-
 Expressions with two variables
Expressions with two variables
Basics of expression with two variables
-
 Example: Evaluating expressions with 2 variables
Example: Evaluating expressions with 2 variables
Evaluating Expressions with Two Variables
-
 Examples of evaluating variable expressions
Examples of evaluating variable expressions
-
 Evaluating an expression in a word problem
Evaluating an expression in a word problem
In this example of evaluating expressions, we're dusting off some geometry. On top of that, it's a word problem. We're seeing how different concepts in math are layered on top of each to create more interesting and complex problems to solve.
Variables and expressions
Wait, why are we using letters in math? How can an 'x' represent a number? What number is it? I must figure this out!!! Yes, you must. This tutorial is great if you're just beginning to delve into the world of algebraic variables and expressions.
-
 Combining like terms
Combining like terms
In simple addition we learned to add all the numbers together to get a sum. In algebra, numbers are sometimes attached to variables and we need to make sure that the variables are alike before we add the numbers.
-
 Adding expressions
Adding expressions
So what if we add not just numbers or variables..but expressions? Here's a simple example to get you thinking about this.
-
 Combining like terms explained
Combining like terms explained
Another good explanation (minus Chuck Norris) on the how we combine like terms in algebra. This will totally make sense.
-
 Combining like terms example 2
Combining like terms example 2
We're going to simplify this expression together putting to use our new knowledge of how to combine like terms. Ok? Let's do it!
-
 Combining like terms, but more complicated
Combining like terms, but more complicated
This example of combining like terms in an expression get a little hairy. Listen closely.
-
 Combining like terms and the distributive property
Combining like terms and the distributive property
We've learned about order of operations and combining like terms. Let's layer the distributive property on top of this.
-
 Applying the distributive property
Applying the distributive property
In this example we are asked to expand an expression using the distributive property. Practice this one with us.
-
 Factoring algebraic expressions
Factoring algebraic expressions
-
 Equivalent forms of expressions
Equivalent forms of expressions
We're looking to find the expressions that are equivalent to a given expression that can be simplified. Give it a try with us.
Manipulating expressions
Using the combined powers of Chuck Norris and polar bears (which are much less powerful than Mr. Norris) to better understand what expressions represent and how we can manipulate them. Great tutorial if you want to understand that expressions are just a way to express things!
-
 Writing simple algebraic expressions
Writing simple algebraic expressions
Can you write the algebraic expressions that represent what these statements are saying? Sure you can! We'll help you.
-
 Writing algebraic expressions
Writing algebraic expressions
These sentences describe or represent algebraic expressions. See if you can translate them for solving. We'll do it together.
-
 Writing algebraic expressions example 2
Writing algebraic expressions example 2
Like other exercises in this tutorial, we're rewriting statements into algebraic expression. This time we have to choose which is the correct one among those given.
-
 Interpreting linear expressions, 1
Interpreting linear expressions, 1
We match the expressions to their meaning in this example. We're reinforcing our knowledge of linear expressions.
-
 Interpreting linear expressions, 2
Interpreting linear expressions, 2
Let's practice matching expressions to their meaning in this example of interpreting linear expressions.
-
 Writing algebraic expressions word problem
Writing algebraic expressions word problem
Here we interpret data in a table and solve a word problem by writing an algebraic expression.
-
 Writing algebraic expressions word problem example 2
Writing algebraic expressions word problem example 2
We're writing an expression to answer a word problem about butter. Could there be a better reason to do this?
-
 Writing algebraic expressions example 3
Writing algebraic expressions example 3
The more you practice, the better you get at writing algebraic expressions. So don't hesitate. Let's go!
Writing and interpreting expressions
All the symbols you write in math are just a language or short-hand to represent real-world ideas. In this tutorial, we'll get experience writing algebraic expressions to elegantly represent real-life ideas.
Algebraic expressions with fractions
Algebraic expressions can be composed of pretty much any operation, including fractions. Here we'll explore how to manipulate fractions algebraically. In some ways this is just a review of adding, subtracting, multiplying and dividing fractions, but now we are doing it with variables!
-
 Why we do the same thing to both sides: Simple equations
Why we do the same thing to both sides: Simple equations
The example of a scale where we try to achieve balance helps to explain why we do the same thing to both sides of an equation.
-
 Representing a relationship with a simple equation
Representing a relationship with a simple equation
Equations are about relationships (no, not girlfriends and boyfriends!) between the two sides of the equation. Let's again use a scale example to help us understand.
-
 One-step equation intuition
One-step equation intuition
This equation can be simplified through a single step to solve for the variable. Can you help?
-
 One step equation intuition introduction
One step equation intuition introduction
To find the value of a variable, you sometimes have to get it on one side of the equation alone. To do that, you'll need to do something to BOTH sides of the equation. Watch. We'll explain why we do this.
-
 Adding and subtracting from both sides of an equation
Adding and subtracting from both sides of an equation
Let's watch as we demonstrate how we add and subtract to both sides of an equation in order to isolate the variable on one side.
-
 Dividing from both sides of an equation
Dividing from both sides of an equation
Let's get a conceptual understanding of why one needs to divide both sides of an equation to solve for a variable.
-
 Solving two-step equations
Solving two-step equations
Here's how we solve a two step equation. It begins with the concept of equality: what we do to one side of the equation must be done to the other.
-
 Why we do the same thing to both sides: Multi-step equations
Why we do the same thing to both sides: Multi-step equations
-
 Why we do the same thing to both sides basic systems
Why we do the same thing to both sides basic systems
-
 Why all the letters in algebra?
Why all the letters in algebra?
Jesse Roe and Sal Khan talk about why we use letters in algebra
The why of algebra
Much of algebra seems obsessed with "doing the same thing to both sides". Why is this? How can we develop an intuition for which algebraic operations are valid and which ones aren't? This tutorial takes a high-level, conceptual walk-through of what an equation represents and why we do the same thing to both sides of it.
-
 Variables and equations word problem: Putting them to work for Super Yoga
Variables and equations word problem: Putting them to work for Super Yoga
Using information from the Super Yoga word problem, explore all the possible combinations and create equations which express the possibilities. Let's figure out which plan is best!
-
 Variables and equations word problem: Which Super Yoga plan is best?
Variables and equations word problem: Which Super Yoga plan is best?
If you're coming to this video before seeing the previous one, back up! Otherwise, we're solving one-step equations to learn which Super Plan is the best value for our budget.
-
 Super Yoga plans: Plotting points
Super Yoga plans: Plotting points
Visualizing the relationship between sessions attended and total cost
-
 Super Yoga plans: Solving systems by substitution
Super Yoga plans: Solving systems by substitution
Continuing our Yoga plan debate by determining where the lines representing the two plans intersect
-
 Super Yoga plans: Solving systems by elimination
Super Yoga plans: Solving systems by elimination
Another way to solve for the number of sessions at which both plans cost the same
Super Yoga plans
This tutorial is a survey of all the core ideas in a traditional first-year algebra course. It is by no means comprehensive (that's what the other 600+ videos are for), but it will hopefully whet your appetite for more algebra!
-
 Variables, expressions, and equations
Variables, expressions, and equations
This video will give you a great understanding of variables, expressions, and equations. If you've struggled with them before, this one may just do the trick!
-
 Substituting variables and judging inequalities
Substituting variables and judging inequalities
In this word problem we're looking to see if various possible answers can be substituted for variables in the expressions, and if the resulting equality holds up. That may actually sound harder than it is, so just jump in with us!
-
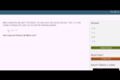 Substituting variables and simple equation
Substituting variables and simple equation
This basic equation asks us to substitute for a variable with given values in order to find correct one.
-
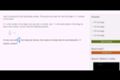 Substituting variables and solving for an equality
Substituting variables and solving for an equality
The great thing about understanding expressions and equalities is that they can be used to solve real life problems, like how many dogs you can eat in a minute!
-
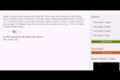 Substituting variables and solving for an inequality
Substituting variables and solving for an inequality
Here's a slightly more complicated expression that seeks not equality, but a greater than relationship. Help us try out different values until we succeed.
-
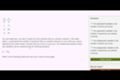 Dependent and independent variables exercise: the basics
Dependent and independent variables exercise: the basics
Here we have a problem that asks us to identify which variables are dependent and independent. Hint: independent variables are not influenced and remain unchanged by the other variable.
-
 Dependent and independent variables exercise: graphing the equation
Dependent and independent variables exercise: graphing the equation
It's helpful to express an equation on a graph where we plot at least 2 points. Watch and we'll show you.
-
 Dependent and independent variables exercise: express the graph as an equation
Dependent and independent variables exercise: express the graph as an equation
We're flipping the last video on its head and doing the opposite. This time we give you the graph and ask you to express it as an equation.
Getting a feel for equations and inequalities
The core underlying concepts in algebra are variables, expressions, equations and inequalities. You will see them throughout your math life (and even life after school). This tutorial won't give you all the tools that you'll later learn to analyze and interpret these ideas, but it'll get you started thinking about them.
 Algebraic expression adding fractions
Algebraic expression adding fractions Algebraic expressions with fraction division
Algebraic expressions with fraction division Treating units algebraically and dimensional analysis
Treating units algebraically and dimensional analysis Figuring out units from formula
Figuring out units from formula Thinking about reasonable units to describe a rate
Thinking about reasonable units to describe a rate Finding the best deal on pesticides
Finding the best deal on pesticides Mileage assumption example
Mileage assumption example