Khan Academy on a Stick
Linear equations
We will now equate two algebraic expressions and think about how it might constrain what value the variables can take on. The algebraic manipulation you learn here really is the heart of algebra.
-
 Why we do the same thing to both sides: Simple equations
Why we do the same thing to both sides: Simple equations
The example of a scale where we try to achieve balance helps to explain why we do the same thing to both sides of an equation.
-
 Representing a relationship with a simple equation
Representing a relationship with a simple equation
Equations are about relationships (no, not girlfriends and boyfriends!) between the two sides of the equation. Let's again use a scale example to help us understand.
-
 One-step equation intuition
One-step equation intuition
This equation can be simplified through a single step to solve for the variable. Can you help?
-
 One step equation intuition introduction
One step equation intuition introduction
To find the value of a variable, you sometimes have to get it on one side of the equation alone. To do that, you'll need to do something to BOTH sides of the equation. Watch. We'll explain why we do this.
-
 Adding and subtracting from both sides of an equation
Adding and subtracting from both sides of an equation
Let's watch as we demonstrate how we add and subtract to both sides of an equation in order to isolate the variable on one side.
-
 Dividing from both sides of an equation
Dividing from both sides of an equation
Let's get a conceptual understanding of why one needs to divide both sides of an equation to solve for a variable.
-
 Solving two-step equations
Solving two-step equations
Here's how we solve a two step equation. It begins with the concept of equality: what we do to one side of the equation must be done to the other.
-
 Why we do the same thing to both sides: Multi-step equations
Why we do the same thing to both sides: Multi-step equations
-
 Why we do the same thing to both sides basic systems
Why we do the same thing to both sides basic systems
The why of algebra
Algebra seems mysterious to me. I really don't "get" what an equation represents. Why do we do the same thing to both sides? This tutorial is a conceptual journey through the basics of algebra. It is made for someone just beginning their algebra adventure. But even folks who feel pretty good that they know how to manipulate equations might pick up a new intuition or two.
-
 Variables and equations word problem: Putting them to work for Super Yoga
Variables and equations word problem: Putting them to work for Super Yoga
Using information from the Super Yoga word problem, explore all the possible combinations and create equations which express the possibilities. Let's figure out which plan is best!
-
 Variables and equations word problem: Which Super Yoga plan is best?
Variables and equations word problem: Which Super Yoga plan is best?
If you're coming to this video before seeing the previous one, back up! Otherwise, we're solving one-step equations to learn which Super Plan is the best value for our budget.
-
 Super Yoga plans: Plotting points
Super Yoga plans: Plotting points
Visualizing the relationship between sessions attended and total cost
-
 Super Yoga plans: Solving systems by substitution
Super Yoga plans: Solving systems by substitution
Continuing our Yoga plan debate by determining where the lines representing the two plans intersect
-
 Super Yoga plans: Solving systems by elimination
Super Yoga plans: Solving systems by elimination
Another way to solve for the number of sessions at which both plans cost the same
-
 Constructing and solving equations in the real world 1 exercise
Constructing and solving equations in the real world 1 exercise
Super Yoga plans
This tutorial is a survey of the major themes in basic algebra in five videos! From basic equations to graphing to systems, it has it all. Great for someone looking for a gentle, but broad understanding of the use of algebra. Also great for anyone unsure of which gym plan they should pick!
-
 Simple equations of the form ax = b
Simple equations of the form ax = b
Let's ease into this, shall we? Here's an introduction to basic algebraic equations of the form ax=b. Remember that you can check to see if you have the right answer by substituting it for the variable!
-
 Simple equations of the form x/a = b
Simple equations of the form x/a = b
Remember that what you do to one side, you have to do to the other. Will you multiply or divide both sides to dump the fraction, x/a? Let's do it together.
-
 Simple equations of the form x + a = b
Simple equations of the form x + a = b
Here's another one-step equation to solve. Unlike the previous two that involved multiplication and division, this one adds a number to the variable. Which operation is opposite of addition?
-
 Simple equations: examples solving a variety of forms
Simple equations: examples solving a variety of forms
Some quick examples to practice solving a variety of one step equations. All 4 operations (add, subtract, multiple, divide) are paired with variables.
-
 Solving a more complicated equation
Solving a more complicated equation
This example demonstrates how we solve an equation expressed such: ax + b = c. It's a little more complicated than previous examples, but you can do it!
-
 Example: two-step equations
Example: two-step equations
Let's practice some two step equations, some of which require merging terms and using the distributive property.
-
 Example: two-step equation with numerator x
Example: two-step equation with numerator x
Solve the equation by isolating the term with numerator x.
Equations for beginners
Like the "Why of algebra" and "Super Yoga plans" tutorials, we'll introduce you to the most fundamental ideas of what equations mean and how to solve them. We'll then do a bunch of examples to make sure you're comfortable with things like 3x – 7 = 8. So relax, grab a cup of hot chocolate, and be on your way to becoming an algebra rockstar. And, by the way, in any of the "example" videos, try to solve the problem on your own before seeing how Sal does it. It makes the learning better!
-
 Linear equation word problem
Linear equation word problem
You'll find that solving linear equations has real world applications. Here's a word problem example that demonstrates that.
-
 Word problem: solving equations
Word problem: solving equations
Here's a nifty word problem in which we find the dimensions of a garden given only the perimeter. Let's create an equation to solve!
Linear equation word problems
Now that we are reasonably familiar with what a linear equation is and how we can solve them, let's apply these skills to tackling real-world problems.
-
 Variables on both sides
Variables on both sides
Equations with the variable on both sides.
-
 Example 1: Variables on both sides
Example 1: Variables on both sides
Multi-step equations 1
-
 Example 2: Variables on both sides
Example 2: Variables on both sides
Solving Equations 2
-
 Understanding steps when solving equations
Understanding steps when solving equations
-
 Figuring out missing algebraic step
Figuring out missing algebraic step
More fancy equations for beginners
You've been through "Equation examples for beginners" and are feeling good. Well, this tutorial continues that journey by addressing equations that are just a bit more fancy. By the end of this tutorial, you really will have some of the core algebraic tools in your toolkit!
Solutions to linear equations
Not every linear equation has exactly one solution. Some have no solutions and others might have an infinite number of solutions. This tutorial will give you the intuition on when these different situations arise.
-
 Rearrange formulas to isolate specific variables
Rearrange formulas to isolate specific variables
Rearrange formulas to isolate specific variables
-
 Solving for a variable
Solving for a variable
Solving for a Variable
-
 Solving for a variable 2
Solving for a variable 2
Solving for a Variable 2
-
 Example: Solving for a variable
Example: Solving for a variable
Example of solving for a variable
-
 Manipulating formula example
Manipulating formula example
Solving for a variable
You feel comfortable solving for an unknown. But life is all about stepping outside of your comfort zone--it's the only way you can grow! This tutorial takes solving equations to another level by making things a little more abstract. You will now solve for a variable, but it will be in terms of other variables. Don't worry, we think you'll find it quite therapeutic once you get the hang of it.
-
 Converting repeating decimals to fractions 1
Converting repeating decimals to fractions 1
Examples of how to convert basic repeating decimals to fractions
-
 Converting repeating decimals to fractions 2
Converting repeating decimals to fractions 2
Converting more interesting repeating decimals to fractions
Converting repeating decimals to fractions
You know that converting a fraction into a decimal can sometimes result in a repeating decimal. For example: 2/3 = 0.666666..., and 1/7 = 0.142857142857... But how do you convert a repeating decimal into a fraction? As we'll see in this tutorial, a little bit of algebra magic can do the trick!
-
 Ex 1 age word problem
Ex 1 age word problem
Imran is 18. Diya is 2. How many years will it take for Imran to be 3 times as old as Diya?
-
 Ex 2 age word problem
Ex 2 age word problem
In 40 years, Imran will be 11 times as old as he is right now. How old is he right now?
-
 Ex 3 age word problem
Ex 3 age word problem
William is 4 times as old as Ben. 12 years ago, William was 7 times as old as Ben. How old is Ben now?
Age word problems
In 72 years, Sal will be 3 times as old as he is today (although he might not be... um... capable of doing much). How old is Sal today? These classic questions have plagued philosophers through the ages. Actually, they haven't. But they have plagued algebra students! Even though few people ask questions like this in the real-world, these are strangely enjoyable problems.
-
 Absolute value equations
Absolute value equations
Absolute Value Equations
-
 Absolute value equations example 1
Absolute value equations example 1
Absolute Value Equations
-
 Absolute value equation example 2
Absolute value equation example 2
Example of solving an absolute value equation
-
 Absolute value equations
Absolute value equations
Absolute Value Equations
-
 Absolute value equations 1
Absolute value equations 1
Absolute Value Equations 1
-
 Absolute value equation example
Absolute value equation example
-
 Absolute value equation with no solution
Absolute value equation with no solution
-
 Absolute value inequalities
Absolute value inequalities
Absolute Value Inequalities
-
 Absolute value inequalities example 1
Absolute value inequalities example 1
Absolute value inequalities, graph solution on number line
-
 Absolute inequalities 2
Absolute inequalities 2
Absolute Inequalities 2
-
 Absolute value inequalities example 3
Absolute value inequalities example 3
Absolute value inequalities 3
Absolute value equations
You are absolutely tired of not knowing how to deal with equations that have absolute values in them. Well, this tutorial might help.
-
 Ex 2: Multi-step equation
Ex 2: Multi-step equation
Turning a non-linear equation into a linear one.
-
 Solving equations with the distributive property
Solving equations with the distributive property
Solving Equations with the Distributive Property
-
 Solving equations with the distributive property 2
Solving equations with the distributive property 2
Solving equations with the distributive property 2
-
 Ex 2: Distributive property to simplify
Ex 2: Distributive property to simplify
Multi-step equations 2
-
 Ex 1: Distributive property to simplify
Ex 1: Distributive property to simplify
Multi-Step Equations
-
 Ex 3: Distributive property to simplify
Ex 3: Distributive property to simplify
Equations with Variables on Both Sides
Simplifying complicated equations
You feel good about your rapidly developing equation-solving ability. Now you're ready to fully flex your brain. In this tutorial, we'll explore equations that don't look so simple at first, but that, with a bit of skill, we can turn into equations that don't cause any stress! Have fun!
-
 Evaluating expressions where individual variable values are unknown
Evaluating expressions where individual variable values are unknown
Working through a few examples where we need to evaluate an expression, but we don't know the individual variable values
-
 Evaluating expressions with unknown variables 2
Evaluating expressions with unknown variables 2
A few more examples where we are asked to evaluate an expression with multiple uknown variables
Evaluating expressions with unknown variables
When solving equations, there is a natural hunger to figure out what an unknown is equal to. This is especially the case if we want to evaluate an expression that the unknown is part of. This tutorial exposes us to a class of solvable problems that challenges this hunger and forces us to be the thinking human beings that we are! In case you're curious, these types of problems are known to show up on standardized exams to see if you are really a thinking human (as opposed to a robot possum).
-
 Mixture problems 2
Mixture problems 2
Mixture problems 2
-
 Basic rate problem
Basic rate problem
Basic Rate Problem
-
 Early train word problem
Early train word problem
Fun word problem that is almost a brain teaser.
-
 Patterns in sequences 1
Patterns in sequences 1
Patterns in Sequences 1
-
 Patterns in sequences 2
Patterns in sequences 2
Patterns in Sequences 2
-
 Equations of sequence patterns
Equations of sequence patterns
Equations of Sequence Patterns
-
 Finding the 100th term in a sequence
Finding the 100th term in a sequence
Finding the 100th Term in a Sequence
-
 Sum of consecutive odd integers
Sum of consecutive odd integers
-
 Challenge example: Sum of integers
Challenge example: Sum of integers
Sum of Consecutive Odd Integers
-
 2003 AIME II problem 1
2003 AIME II problem 1
2003 AIME II Problem 1
-
 Bunch of examples
Bunch of examples
-
 Mixture problems 3
Mixture problems 3
Mixture problems 3
More equation practice
This tutorial is for you if you already have the basics of solving equations and are looking to put your newfound powers to work in more examples.
-
 Order of operations, more examples
Order of operations, more examples
Here we have a series of order of operations problems demonstrated in succession so you can really nail down this concept.
-
 Algebra: Linear equations 1
Algebra: Linear equations 1
equations of the form AX=B
-
 Algebra: Linear equations 2
Algebra: Linear equations 2
solving equations of the form AX+B=C
-
 Algebra: Linear equations 3
Algebra: Linear equations 3
Linear equations with multiple variable and constant terms
-
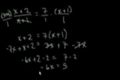 Algebra: Linear equations 4
Algebra: Linear equations 4
Solving linear equations with variable expressions in the denominators of fractions
-
 Averages
Averages
Introduction to averages and algebra problems involving averages.
-
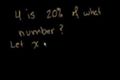 Taking percentages
Taking percentages
Taking a percentage of a number.
-
 Growing by a percentage
Growing by a percentage
In this example we grow a whole number by a percentage of itself. Growing by percentage is a common skill often used when figuring how much is owed or earned with interest.
-
 More percent problems
More percent problems
Slightly harder percent problems
-
 Age word problems 1
Age word problems 1
Age word problems
-
 Age word problems 2
Age word problems 2
Second set of age word problems
-
 Age word problems 3
Age word problems 3
Part 3 of the presentation on age word problems
Old school equations with Sal
Some of Sal's oldest (and roughest) videos on algebra. Great tutorial if you want to see what Khan Academy was like around 2006. You might also like it if you feel like Sal has lost his magic now that he doesn't use the cheapest possible equipment to make the videos.
 Equation special cases
Equation special cases Number of solutions to linear equations
Number of solutions to linear equations Number of solutions to linear equations ex 3
Number of solutions to linear equations ex 3 Number of solutions to linear equations ex 2
Number of solutions to linear equations ex 2