Right triangles and trigonometry : Khan Academy on a Stick

Khan Academy on a Stick

Geometry

Introduction to Euclidean geometry
Angles and intersecting lines
Congruence
Similarity
Right triangles and trigonometry
Perimeter, area, and volume
Circles
Special properties and parts of triangles
Quadrilaterals
Transformations
Analytic geometry
Geometric constructions
Worked examples

Pythagorean theorem
Pythagorean Theorem
The Pythagorean theorem intro
Introduction to the Pythagorean Theorem
Pythagorean theorem 1
Pythagorean Theorem 1
Pythagorean theorem 2
Pythagorean Theorem 2
Pythagorean theorem 3
Pythagorean Theorem 3
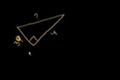Introduction to the Pythagorean theorem
Right triangles and the Pythagorean Theorem
Pythagorean theorem II
More Pythagorean Theorem examples. Introduction to 45-45-90 triangles.

Pythagorean theorem

Named after the Greek philosopher who lived nearly 2600 years ago, the Pythagorean theorem is as good as math theorems get (Pythagoras also started a religious movement). It's simple. It's beautiful. It's powerful. In this tutorial, we will cover what it is and how it can be used. We have another tutorial that gives you as many proofs of it as you might need.

Garfield's proof of the Pythagorean theorem
James Garfield's proof of the Pythagorean Theorem.
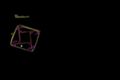Bhaskara's proof of the Pythagorean theorem
An elegant visual proof of the Pythagorean Theorem developed by the 12th century Indian mathematician Bhaskara.
Pythagorean theorem proof using similarity
Proof of the Pythagorean Theorem using similarity
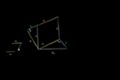Another Pythagorean theorem proof
Visually proving the Pythagorean Theorem

Pythagorean theorem proofs

The Pythagorean theorem is one of the most famous ideas in all of mathematics. This tutorial proves it. Then proves it again... and again... and again. More than just satisfying any skepticism of whether the Pythagorean theorem is really true (only one proof would be sufficient for that), it will hopefully open your mind to new and beautiful ways to prove something very powerful.

30-60-90 triangle side ratios proof
Proving the ratios between the sides of a 30-60-90 triangle
45-45-90 triangle side ratios
Showing the ratios of the sides of a 45-45-90 triangle are 1:1:sqrt(2)
30-60-90 triangle example problem
Using what we know about 30-60-90 triangles to solve what at first seems to be a challenging problem
Area of a regular hexagon
Using what we know about triangles to find the area of a regular hexagon
45-45-90 triangles
Introduction to 45-45-90 Triangles
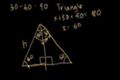Intro to 30-60-90 triangles
A few more 45-45-90 examples and an introduction to 30-60-90 triangles.

Special right triangles

We hate to pick favorites, but there really are certain right triangles that are more special than others. In this tutorial, we pick them out, show why they're special, and prove it! These include 30-60-90 and 45-45-90 triangles (the numbers refer to the measure of the angles in the triangle).

Basic trigonometry
Introduction to trigonometry
Example: Using soh cah toa
Worked example evaluating sine and cosine using soh cah toa definition.
Basic trigonometry II
A few more examples using SOH CAH TOA
Example: Trig to solve the sides and angles of a right triangle
Worked example using trigonometry to solve for the lengths of the sides of a right triangle given one of the non-right angles.
Angle to aim to get alien
How much of a pyramid is submerged

Sine, cosine and tangent trigonometric functions

In this tutorial, you will learn all the trigonometry that you are likely to remember in ten years (assuming you are a lazy non-curious, non-lifelong learner). But even in that non-ideal world where you forgot everything else, you'll be able to do more than you might expect with the concentrated knowledge you are about to get.

Trig ratios and similarity

In this tutorial, we will build on our understanding of similarity to get a deeper appreciation for the motivation behind trigonometric ratios and relationships.