Khan Academy on a Stick
Congruence
If you can take one figure and flip, shift and rotate (not resize) it to be identical to another figure, then the two figures are congruent. This topic explores this foundational idea in geometry.
Transformations and congruence
Two figures are congruent if you can go from one to another through some combination of translations, reflections and rotations. In this tutorial, we'll really internalize this by working through the actual transformations.
-
 Congruent triangles and SSS
Congruent triangles and SSS
What it means for triangles to be congruent
-
 SSS to show a radius is perpendicular to a chord that it bisects
SSS to show a radius is perpendicular to a chord that it bisects
More on the difference between a theorem and axiom. Proving a cool result using SSS
-
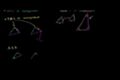 Other triangle congruence postulates
Other triangle congruence postulates
SSS, SAS, ASA and AAS postulates for congruent triangles. Showing AAA is only good for similarity and SSA is good for neither
-
 Two column proof showing segments are perpendicular
Two column proof showing segments are perpendicular
Using triangle congruency postulates to show that two intersecting segments are perpendicular
-
 Finding congruent triangles
Finding congruent triangles
Using the SSS, ASA, SAS, and AAS postulates to find congruent triangles
-
 More on why SSA is not a postulate
More on why SSA is not a postulate
SSA special cases including RSH
-
 Perpendicular radius bisects chord
Perpendicular radius bisects chord
Simple proof using RSH postulate to show that a radius perpendicular to a chord bisects it
-
 Congruent triangle proof example
Congruent triangle proof example
Proving that a point is the midpoint via triangle congruency
-
 Congruent triangle example 2
Congruent triangle example 2
Showing that segments have the same length
-
 Figuring out all the angles for congruent triangles example
Figuring out all the angles for congruent triangles example
Another example of using congruency to figure out a bunch of angles
-
 Problem involving angle derived from square and circle
Problem involving angle derived from square and circle
Challenging problem to find an angle
Congruence postulates
We begin to seriously channel Euclid in this tutorial to really, really (no, really) prove things--in particular, that triangles are congruents. You'll appreciate (and love) what rigorous proofs are. It will sharpen your mind and make you a better friend, relative and citizen (and make you more popular in general). Don't have too much fun.
-
 Congruent legs and base angles of isosceles triangles
Congruent legs and base angles of isosceles triangles
Showing that congruent legs imply equal base angles and vice versa
-
 Equilateral triangle sides and angles congruent
Equilateral triangle sides and angles congruent
Showing that all of the angles of an equilateral triangle are 60 degrees
-
 Equilateral and isosceles example problems
Equilateral and isosceles example problems
Three example problems involving isosceles and equilateral triangles. 2 from Art of Problem Solving (by Richard Rusczyk) book
-
 Another isosceles example problem
Another isosceles example problem
Possible angles for an isosceles triangle
-
 Example involving an isosceles triangle and parallel lines
Example involving an isosceles triangle and parallel lines
Integrating what we know about isosceles triangles and parallel lines
Congruence and isosceles and equilateral triangles
This tutorial uses our understanding of congruence postulates to prove some neat properties of isosceles and equilateral triangles.
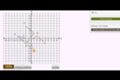 Testing congruence by transformations example
Testing congruence by transformations example Another congruence by transformation example
Another congruence by transformation example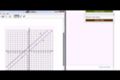 Example of rigid transformation and congruence
Example of rigid transformation and congruence Another example of rigid transformations for congruence
Another example of rigid transformations for congruence