Khan Academy on a Stick
Functions and their graphs
Revisiting what a function is and how we can define and visualize one.
-
 What is a function?
What is a function?
-
 Difference between equations and functions
Difference between equations and functions
Jesse Roe and Sal talk about the difference between equations and functions
-
 Relations and functions
Relations and functions
Relations and Functions
-
 Evaluating with function notation
Evaluating with function notation
Linear Function Graphs
-
 Understanding function notation (example 1)
Understanding function notation (example 1)
-
 Understanding function notation (example 2)
Understanding function notation (example 2)
-
 Understanding function notation (example 3)
Understanding function notation (example 3)
Function introduction
Relationships can be any association between sets of numbers while functions have only one output for a given input. This tutorial works through a bunch of examples of testing whether something is a valid function. As always, we really encourage you to pause the videos and try the problems before Sal does!
-
 Sum of functions
Sum of functions
Sum of Functions
-
 Difference of functions
Difference of functions
Difference of Functions
-
 Product of functions
Product of functions
Product of Functions
-
 Quotient of functions
Quotient of functions
Quotient of functions and factoring by grouping
-
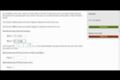 Modeling with combined functions
Modeling with combined functions
Find the value of a function for a given x based on a graph, and perform operations with that value.
Function expressions
We'll now see what it means to add, subtract, multiply and divide functions!
-
 Domain of a function
Domain of a function
Figuring out the domain of a function
-
 Domain and range of a relation
Domain and range of a relation
Domain and Range of a Relation
-
 Domain and range of a function given a formula
Domain and range of a function given a formula
Domain and Range of a Function Given a Formula
-
 Domain and range 1
Domain and range 1
Domain and Range 1
-
 Domain of a radical function
Domain of a radical function
Domain of a Radical Function
-
 Domain and range 2
Domain and range 2
Domain and Range 2
-
 Domain and range of a function
Domain and range of a function
Domain and range
What values can you and can you not input into a function? What values can the function output? The domain is the set of values that the function is defined for (i.e., the values that you can input into a function). The range is the set of values that the function output can take on. This tutorial covers the ideas of domain and range through multiple worked examples. These are really important ideas as you study higher mathematics.
-
 Testing if a relationship is a function
Testing if a relationship is a function
Testing if a relationship is a function
-
 Graphical relations and functions
Graphical relations and functions
Graphical Relations and Functions
-
 Functions as graphs
Functions as graphs
-
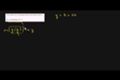 Recognizing functions (example 1)
Recognizing functions (example 1)
-
 Recognizing functions (example 2)
Recognizing functions (example 2)
-
 Functional relationships 1
Functional relationships 1
Functional Relationships 1
-
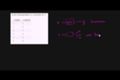 Recognizing functions (example 3)
Recognizing functions (example 3)
-
 Recognizing functions (example 4)
Recognizing functions (example 4)
-
 Recognizing functions (example 5)
Recognizing functions (example 5)
Recognizing functions
Not all relationships are functions. In this tutorial, you'll learn which are!
-
 Introduction to function inverses
Introduction to function inverses
Introduction to Function Inverses
-
 Function inverse example 1
Function inverse example 1
Function Inverse Example 1
-
 Function inverses example 2
Function inverses example 2
Function Inverses Example 2
-
 Function inverses example 3
Function inverses example 3
Function Inverses Example 3
Function inverses
Functions associate a set of inputs with a set of outputs (in fancy language, they "map" one set to another). But can we go the other way around? Are there functions that can start with the outputs as inputs and produce the original inputs as outputs? Yes, there are! They are called function inverses! This tutorial works through a bunch of examples to get you familiar with the world of function inverses.
Piecewise functions
In this tutorial, we will get practice looking at wackier functions that are defined interval by interval (or piece by piece)!
-
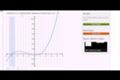 When a function is positive or negative
When a function is positive or negative
-
 Recognizing odd and even functions
Recognizing odd and even functions
Even and odd functions
-
 Connection between even and odd numbers and functions
Connection between even and odd numbers and functions
A possible reason why even functions are called "even" and odd functions are called "odd"
-
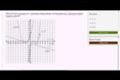 Recognizing features of functions (example 1)
Recognizing features of functions (example 1)
-
 Recognizing features of functions (example 2)
Recognizing features of functions (example 2)
-
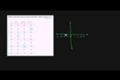 Recognizing features of functions (example 3)
Recognizing features of functions (example 3)
Properties and features of functions
You know a function when you see one, but are curious to start looking deeper at their properties. Some functions seem to be mirror images around the y-axis while others seems to be flipped mirror images while others are neither. How can we shift and reflect them? This tutorial addresses these questions by covering even and odd functions. It also covers how we can shift and reflect them. Enjoy!
Comparing and interpreting functions
In this tutorial, we'll dive deeper into actually thinking about what functions represent and how one function compares to another.
-
 Why dividing by zero is undefined
Why dividing by zero is undefined
Thinking about why dividing by zero is left undefined
-
 Why zero divided by zero is undefined/indeterminate
Why zero divided by zero is undefined/indeterminate
Multiple arguments for what we could get when we divide zero by zero. We will later see that this can be considered indeterminate
-
 Undefined and indeterminate
Undefined and indeterminate
Why 0/0 is considered to be indeterminate
Undefined and indeterminate answers
In second grade you may have raised your hand in class and asked what you get when you divide by zero. The answer was probably "it's not defined." In this tutorial we'll explore what that (and "indeterminate") means and why the math world has left this gap in arithmetic. (They could define something divided by 0 as 7 or 9 or 119.57 but have decided not to.)
-
 A more formal understanding of functions
A more formal understanding of functions
A more formal understanding of functions
-
 Introduction to the inverse of a function
Introduction to the inverse of a function
Introduction to the inverse of a function
More mathy functions
In this tutorial, we'll start to use and define functions in more "mathy" or formal ways.
 Introduction to function composition
Introduction to function composition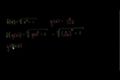 Creating new function from composition
Creating new function from composition Evaluating composite functions example
Evaluating composite functions example Modeling with function composition
Modeling with function composition Graphs of absolute value functions
Graphs of absolute value functions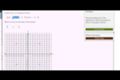 Absolute value graphing exercise example
Absolute value graphing exercise example Matching expressions to define intervals of functions example
Matching expressions to define intervals of functions example Finding a piecewise function definition from graph
Finding a piecewise function definition from graph Shifting and reflecting functions
Shifting and reflecting functions Shifting functions
Shifting functions Flipping and shifting radical functions
Flipping and shifting radical functions Equations for radical functions example
Equations for radical functions example Matching radical functions with graphs exercise example
Matching radical functions with graphs exercise example Interpreting features of functions (example 1)
Interpreting features of functions (example 1) Interpreting features of functions (example 2)
Interpreting features of functions (example 2) Comparing features of functions (example 1)
Comparing features of functions (example 1) Comparing features of functions (example 2)
Comparing features of functions (example 2) Comparing features of functions (example 3)
Comparing features of functions (example 3)