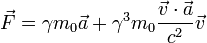Newton's laws of motion
Did you know...
Arranging a Wikipedia selection for schools in the developing world without internet was an initiative by SOS Children. SOS Children works in 45 African countries; can you help a child in Africa?
| Classical mechanics |
|---|
|
|
Branches
|
|
Formulations
Newtonian mechanics
(Vectorial mechanics) Analytical mechanics ( Lagrangian mechanics
Hamiltonian mechanics) |
|
Fundamental concepts
|
|
Core topics
Rigid body
Newton's law of
universal gravitation
Inertial / Non-inertial
reference frame
Mechanics of planar
particle motion
|
|
Rotational motion
Circular motion
Centrifugal force
|
Newton's laws of motion are three physical laws which provide relationships between the forces acting on a body and the motion of the body. They were first compiled by Sir Isaac Newton in his work Philosophiae Naturalis Principia Mathematica ( 1687). The laws form the basis for classical mechanics and Newton himself used them to explain many results concerning the motion of physical objects. In the third volume of the text, Newton showed that these laws of motion, combined with his law of universal gravitation, explained Kepler's laws of planetary motion.
Traditional brief statements of the three laws:
- A physical body will remain at rest, or continue to move at a constant velocity, unless an outside net force acts upon it.
- The net force on a body is equal to its mass multiplied by its acceleration.
- To every action there is an equal and opposite reaction.
The three laws in detail
Newton's laws of motion describe the acceleration of massive particles. In modern language, the laws may be stated as:
- First law
- If no net force acts on a particle, then it is possible to select a set of reference frames, called inertial reference frames, observed from which the particle moves without any change in velocity. This law is often simplified into the sentence "An object will stay at rest or continue at a constant velocity unless acted upon by an external unbalanced force".
- Second law
- Observed from an inertial reference frame, the net force on a particle is proportional to the time rate of change of its linear momentum:
![F = d[mv]/dt](../../images/195/19519.png) . Momentum is the product of mass and velocity. When the mass is constant, this law is often stated as
. Momentum is the product of mass and velocity. When the mass is constant, this law is often stated as 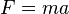 (the net force on an object is equal to the mass of the object multiplied by its acceleration).
(the net force on an object is equal to the mass of the object multiplied by its acceleration). - Third law
- Whenever a particle A exerts a force on another particle B, B simultaneously exerts a force on A with the same magnitude in the opposite direction. The strong form of the law further postulates that these two forces act along the same line. This law is often simplified into the sentence "Every action has an equal and opposite reaction".
In the given interpretation mass, acceleration, and, most importantly, force are assumed to be externally defined quantities. This is the most common, but not the only interpretation: one can consider the laws to be a definition of these quantities. Notice that the second law only holds when the observation is made from an inertial reference frame, and since an inertial reference frame is defined by the first law, asking a proof of the first law from the second law is a logical fallacy.
Newton's first law: law of inertia
Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed.
This law is also called the law of inertia.
This is often paraphrased as "zero net force implies zero acceleration", but this is an over-simplification. As formulated by Newton, the first law is more than a special case of the second law. Newton arranged his laws in hierarchical order for good reason (e.g. see Gailili & Tseitlin 2003). Essentially, the first law establishes frames of reference for which the other laws are applicable, such frames being called inertial frames. To understand why this is required, consider a ball at rest within an accelerating body: an aeroplane on a runway will suffice for this example. From the perspective of anyone within the aeroplane (that is, from the aeroplane's frame of reference when put in technical terms) the ball will appear to move backwards as the plane accelerates forwards (the same feeling of being pushed back into your seat as the plane accelerates). This appears to contradict Newton's second law as, from the point of view of the passengers, there appears to be no force acting on the ball which would cause it to move. The reason why there is in fact no contradiction is because Newton's second law (without modification) is not applicable in this situation because Newton's first law was never applicable in this situation (i.e. the stationary ball does not remain stationary). Thus, it is important to establish when the various laws are applicable or not since they are not applicable in all situations. On a more technical note, although Newton's laws are not applicable on non-inertial frames of reference, such as the accelerating aeroplane, they can be made to do so with the introduction of a " fictitious force" acting on the entire system: basically, by introducing a force that quantifies the anomalous motion of objects within that system (such as the ball moving without an apparent influence in the example above).
The net force on an object is the vector sum of all the forces acting on the object. Newton's first law says that if this sum is zero, the state of motion of the object does not change. Essentially, it makes the following two points:
- An object that is not moving will not move until a net force acts upon it.
- An object that is in motion will not change its velocity (accelerate) until a net force acts upon it.
The first point seems relatively obvious to most people, but the second may take some thinking through, because we have no experience in every-day life of things that keep moving forever (except celestial bodies). If one slides a hockey puck along a table, it doesn't move forever, it slows and eventually comes to a stop. But according to Newton's laws, this is because a force is acting on the hockey puck and, sure enough, there is frictional force between the table and the puck, and that frictional force is in the direction opposite the movement. It is this force which causes the object to slow to a stop. In the absence of such a force, as approximated by an air hockey table or ice rink, the puck's motion would not slow. Newton's first law is just a restatement of what Galileo had already described and Newton gave credit to Galileo. It differs from Aristotle's view that all objects have a natural place in the universe. Aristotle believed that heavy objects like rocks wanted to be at rest on the Earth and that light objects like smoke wanted to be at rest in the sky and the stars wanted to remain in the heavens.
However, a key difference between Galileo's idea and Aristotle's is that Galileo realized that force acting on a body determines acceleration, not velocity. This insight leads to Newton's First Law—no force means no acceleration, and hence the body will maintain its velocity.
The Law of Inertia apparently occurred to several different natural philosophers and scientists independently. The inertia of motion was described in the 3rd century BC by the Chinese philosopher Mo Tzu, and in the 11th century by the Muslim scientists, Alhazen and Avicenna. The 17th century philosopher René Descartes also formulated the law, although he did not perform any experiments to confirm it.
There are no perfect demonstrations of the law, as friction usually causes a force to act on a moving body, and even in outer space gravitational forces act and cannot be shielded against, but the law serves to emphasize the elementary causes of changes in an object's state of motion:
Newton's second law: law of acceleration
Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.
The rate of change of momentum of a body is proportional to the resultant force acting on the body and is in the same direction.
In Motte's 1729 translation (from Newton's Latin), the second law of motion reads:
LAW II: The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed. — If a force generates a motion, a double force will generate double the motion, a triple force triple the motion, whether that force be impressed altogether and at once, or gradually and successively. And this motion (being always directed the same way with the generating force), if the body moved before, is added to or subtracted from the former motion, according as they directly conspire with or are directly contrary to each other; or obliquely joined, when they are oblique, so as to produce a new motion compounded from the determination of both.
Using modern symbolic notation, Newton's second law can be written as a vector differential equation:
where:
The product of the mass and velocity is the momentum of the object (which Newton himself called "quantity of motion"). The use of algebraic expressions became popular during the 18th century, after Newton's death, while vector notation dates to the late 19th century. The Principia expresses mathematical theorems in words and consistently uses geometrical rather than algebraic proofs.
If the mass of the object in question is constant this differential equation can be rewritten as:
where:
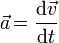 is the acceleration.
is the acceleration.
A verbal equivalent of this is "the acceleration of an object is proportional to the force applied, and inversely proportional to the mass of the object". If momentum varies nonlinearly with velocity (as it does for high velocities—see special relativity), then this last version is not accurate.
Taking special relativity into consideration, the equation becomes
where:
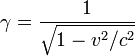
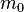 is the rest mass or invariant mass.
is the rest mass or invariant mass. is the speed of light.
is the speed of light.
Note that force depends on speed of the moving body, acceleration, and its rest mass. However, when the speed of the moving body is much lower than the speed of light, the equation above reduces to the familiar 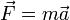 .
.
Mass must always be taken as constant in classical mechanics. So-called variable mass systems like a rocket can not be directly treated by making mass a function of time in the second law. The reasoning, given in An Introduction to Mechanics by Kleppner and Kolenkow and other modern texts, is excerpted here:
- Newton's second law applies fundamentally to particles. In classical mechanics, particles by definition have constant mass. In case of well-defined systems of particles, Newton's law can be extended by integrating over all the particles in the system. In this case, we have to refer all vectors to the centre of mass. Applying the second law to extended objects implicitly assumes the object to be a well-defined collection of particles. However, 'variable mass' systems like a rocket or a leaking bucket do not consist of a set number of particles. They are not well-defined systems. Therefore Newton's second law can not be applied to them directly. The naïve application of F = dp/dt will usually result in wrong answers in such cases. However, applying the conservation of momentum to a complete system (such as a rocket and fuel, or a bucket and leaked water) will give unambiguously correct answers.
Newton's third law: law of reciprocal actions
Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi.
All forces occur in pairs, and these two forces are equal in magnitude and opposite in direction.
This law of motion is commonly paraphrased as: "For every force there is an equal, but opposite, force".
A more direct translation is:
LAW III: To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts. — Whatever draws or presses another is as much drawn or pressed by that other. If you press a stone with your finger, the finger is also pressed by the stone. If a horse draws a stone tied to a rope, the horse (if I may so say) will be equally drawn back towards the stone: for the distended rope, by the same endeavour to relax or unbend itself, will draw the horse as much towards the stone, as it does the stone towards the horse, and will obstruct the progress of the one as much as it advances that of the other. If a body impinge upon another, and by its force change the motion of the other, that body also (because of the equality of the mutual pressure) will undergo an equal change, in its own motion, toward the contrary part. The changes made by these actions are equal, not in the velocities but in the motions of the bodies; that is to say, if the bodies are not hindered by any other impediments. For, as the motions are equally changed, the changes of the velocities made toward contrary parts are reciprocally proportional to the bodies. This law takes place also in attractions, as will be proved in the next scholium.
In the above, as usual, motion is Newton's name for momentum, hence his careful distinction between motion and velocity.
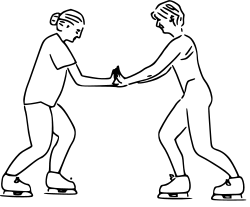
As shown in the diagram opposite, the skaters' forces on each other are equal in magnitude, and opposite in direction. Although the forces are equal, the accelerations are not: the less massive skater will have a greater acceleration due to Newton's second law. It is important to note that the action/reaction pair act on different objects and do not cancel each other out. The two forces in Newton's third law are of the same type, e.g., if the road exerts a forward frictional force on an accelerating car's tires, then it is also a frictional force that Newton's third law predicts for the tires pushing backward on the road.
Newton used the third law to derive the law of conservation of momentum; however from a deeper perspective, conservation of momentum is the more fundamental idea (derived via Noether's theorem from Galilean invariance), and holds in cases where Newton's third law appears to fail, for instance when force fields as well as particles carry momentum, and in quantum mechanics.
Importance and range of validity
Newton's laws were verified by experiment and observation for over 200 years, and they are excellent approximations at the scales and speeds of everyday life. Newton's laws of motion, together with his law of universal gravitation and the mathematical techniques of calculus, provided for the first time a unified quantitative explanation for a wide range of physical phenomena.
These three laws hold to a good approximation for macroscopic objects under everyday conditions. However, Newton's laws (combined with Universal Gravitation and Classical Electrodynamics) are inappropriate for use in certain circumstances, most notably at very small scales, very high speeds (in special relativity, the Lorentz factor must be included in the expression for momentum along with rest mass and velocity) or very strong gravitational fields. Therefore, the laws cannot be used to explain phenomena such as conduction of electricity in a semiconductor, optical properties of substances, errors in non-relativistically corrected GPS systems and superconductivity. Explanation of these phenomena requires more sophisticated physical theory, including General Relativity and Relativistic Quantum Mechanics.
In quantum mechanics concepts such as force, momentum, and position are defined by linear operators that operate on the quantum state; at speeds that are much lower than the speed of light, Newton's laws are just as exact for these operators as they are for classical objects. At speeds comparable to the speed of light, the second law holds in the original form 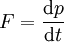 , which says that the force is the derivative of the momentum of the object with respect to time, but some of the newer versions of the second law (such as the constant mass approximation above) do not hold at relativistic velocities.
, which says that the force is the derivative of the momentum of the object with respect to time, but some of the newer versions of the second law (such as the constant mass approximation above) do not hold at relativistic velocities.
Relationship to the conservation laws
In modern physics, the laws of conservation of momentum, energy, and angular momentum are of more general validity than Newton's laws, since they apply to both light and matter, and to both classical and non-classical physics.
This can be stated simply, "[Momentum, energy, angular momentum, matter] cannot be created or destroyed."
Because force is the time derivative of momentum, the concept of force is redundant and subordinate to the conservation of momentum, and is not used in fundamental theories (e.g. quantum mechanics, quantum electrodynamics, general relativity, etc.). The standard model explains in detail how the three fundamental forces known as gauge forces originate out of exchange by virtual particles. Other forces such as gravity and fermionic degeneracy pressure arise from conditions in the equations of motion in the underlying theories.
Newton stated the third law within a world-view that assumed instantaneous action at a distance between material particles. However, he was prepared for philosophical criticism of this action at a distance, and it was in this context that he stated the famous phrase " I feign no hypotheses". In modern physics, action at a distance has been completely eliminated, except for subtle effects involving quantum entanglement.
Conservation of energy was discovered nearly two centuries after Newton's lifetime, the long delay occurring because of the difficulty in understanding the role of microscopic and invisible forms of energy such as heat and infra-red light.

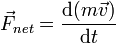
 is the
is the  is
is  is the
is the 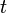 is
is