|
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.
|
Summary
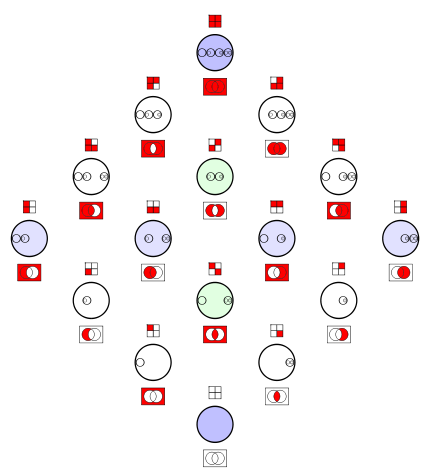
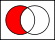
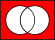
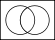
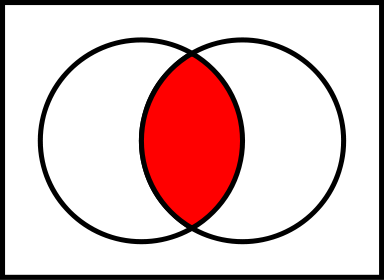
One of 16 Venn diagrams, representing 2-ary Boolean functions like set operations and logical connectives:
Operations and relations in set theory and logic
|
|
|
|
∅c |
|
|
|
|
|
|
|
A = A |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
Ac 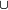 Bc Bc |
true
A ↔ A |
A 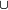 B B |
|
|
|
|
|
A 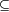 Bc Bc |
A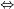 A A
|
A 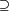 Bc Bc |
|
|
|
|
|
 |
|
 |
|
|
|
|
|
 |
|
 |
|
|
|
|
A 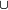 Bc Bc |
¬A  ¬B ¬B
A → ¬B |
A 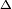 B B |
A  B B
A ← ¬B |
Ac 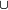 B B |
|
|
|
A 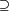 B B |
A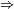 ¬B ¬B
|
A = Bc |
A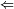 ¬B ¬B
|
A 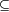 B B |
|
|
|
 |
|
 |
|
 |
|
|
|
 |
|
 |
|
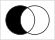 |
|
Bc |
A  ¬B ¬B
A ← B |
A |
A  B B
A ↔ ¬B |
Ac |
¬A  B B
A → B |
B |
|
B = ∅ |
A B B
|
A = ∅c |
A ¬B ¬B
|
A = ∅ |
A B B
|
B = ∅c |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
¬B
|
A  Bc Bc |
A
|
(A  B)c B)c |
¬A
|
Ac  B B |
B
|
|
B false false
|
|
A true true
|
A = B |
A false false
|
|
B true true
|
|
|
 |
|
 |
|
 |
|
|
|
 |
|
 |
|
 |
|
|
|
A  ¬B ¬B
|
Ac  Bc Bc |
A  B B
|
A  B B |
¬A  B B
|
|
|
|
|
|
A B B
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
 |
|
 |
|
|
|
|
|
¬A  ¬B ¬B
|
∅ |
A  B B
|
|
|
|
|
|
|
A = Ac |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
false
A ↔ ¬A |
|
|
|
|
|
|
|
A ¬A ¬A
|
|
|
|
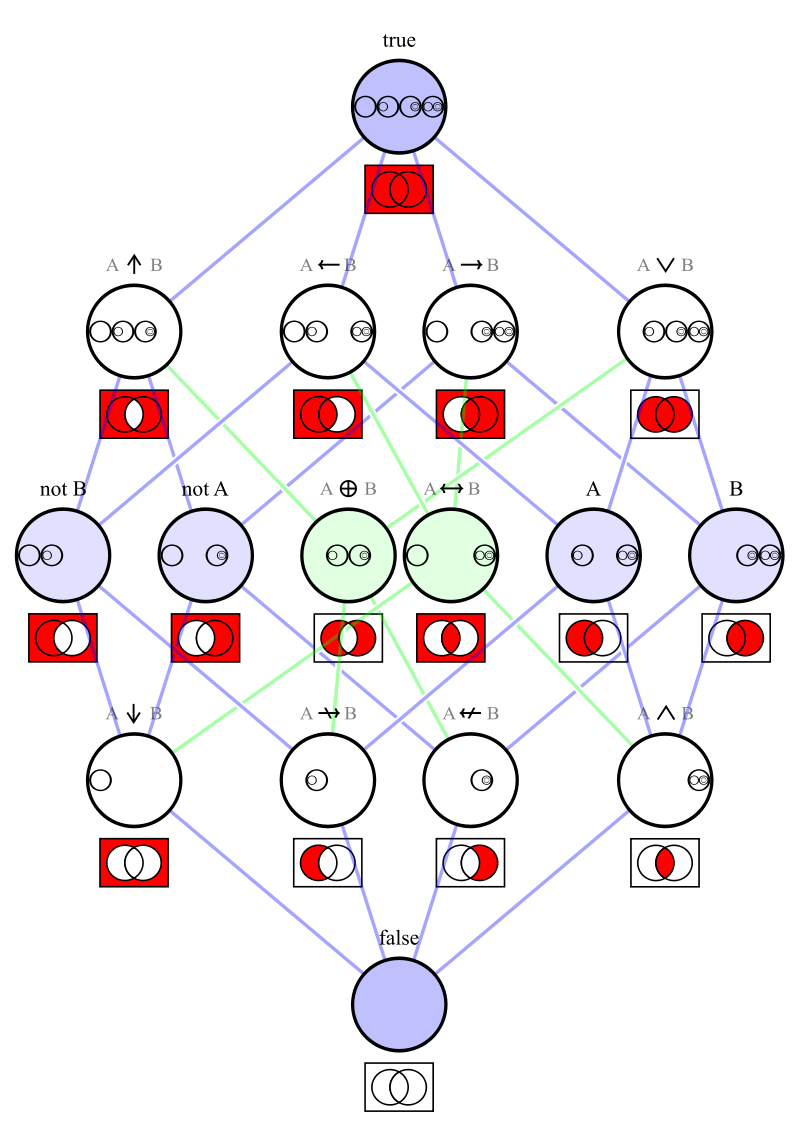
These sets or statements have complements
or negations. They are shown inside this matrix. |
These relations are statements, and have negations.
They are shown in a seperate matrix in the box below. |
| more relations |
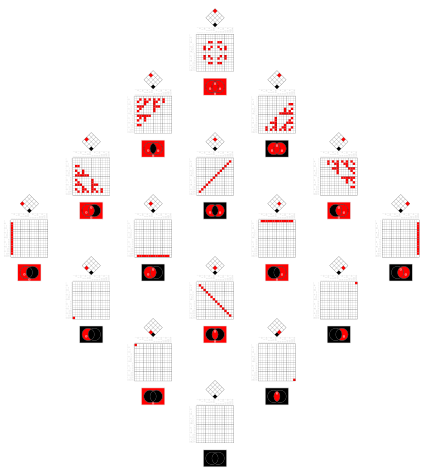
The operations, arranged in the same matrix as above.
The 2x2 matrices show the same information like the Venn diagrams.
(This matrix is similar to this Hasse diagram.)
In set theory the Venn diagrams represent the set,
which is marked in red.
|
These 15 relations, except the empty one, are minterms and can be the case.
The relations in the files below are disjunctions. The red fields of their 4x4 matrices tell, in which of these cases the relation is true.
(Inherently only conjunctions can be the case. Disjunctions are true in several cases.)
In set theory the Venn diagrams tell,
that there is an element in every red,
and there is no element in any black intersection. |
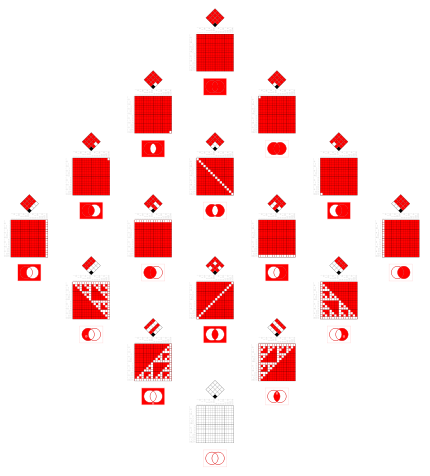
Negations of the relations in the matrix on the right.
In the Venn diagrams the negation exchanges black and red.
In set theory the Venn diagrams tell,
that there is an element in one of the red intersections.
(The existential quantifications for the red intersections are combined by or.
They can be combined by the exclusive or as well.) |
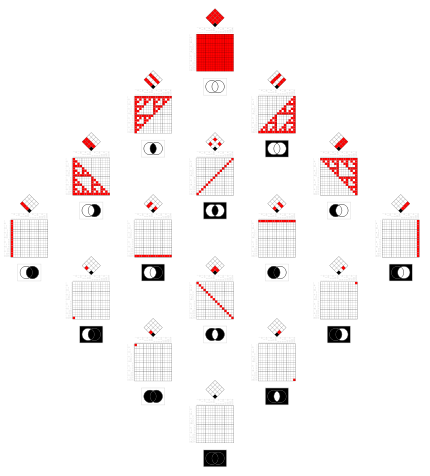
Relations like subset and implication,
arranged in the same kind of matrix as above.
In set theory the Venn diagrams tell,
that there is no element in any black intersection.
|
|
| Public domainPublic domainfalsefalse |
 |
This file is ineligible for copyright and therefore in the public domain, because it consists entirely of information that is common property and contains no original authorship. |
File usage
The following pages on Schools Wikipedia link to this image (list may be incomplete):
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it. If the file has been modified from its original state, some details may not fully reflect the modified file.
SOS Childrens Villages has brought Wikipedia to the classroom. SOS Childrens Villages helps those who have nothing and no one, giving them back the famly they have lost and bringing them the very best opportunities for a happy, healthy future. Sponsoring a child is the coolest way to help.


 Bc
Bc Bc
Bc A
A Bc
Bc ¬B
¬B B
B ¬B
¬B ¬B
¬B B
B Bc
Bc ¬B
¬B B
B