
File:Chaotic Bunimovich stadium.png
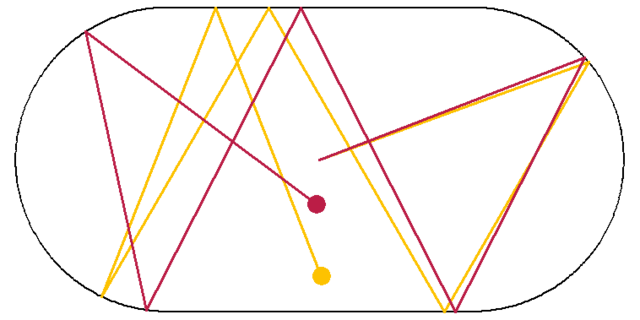
Size of this preview: 640 × 320 pixels.
| |
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help. |
Summary
| Description |
English: billiards in a Bunimovich stadium, initial deviation is an angle of one degree
Mathematica source code In[403]:= NN[v_]:=Sqrt[v[[1]]^2+v[[2]]^2]; Ang[v0_,va_,vb_]:=(va-v0).(vb-v0)/NN[va-v0]/NN[vb-v0]; 1st trajectory p0={0,0}; q0=\[Pi]/9; In[334]:= NSolve[(p0[[1]]+t Cos[q0]-1)^2+(p0[[2]]+t Sin[q0])^2==1,t] Out[334]= {{t\[Rule]0.},{t\[Rule]1.87939}} In[335]:= t0=1.8793852415718169`; p1=p0+t0{Cos[q0],Sin[q0]}; q1=-\[Pi]+(ArcCos[p1[[1]]-1]+q0); NSolve[p1[[2]]+t Sin[q1]\[Equal]-1,t] Out[338]= {{t\[Rule]1.89693}} In[180]:= t1=1.896927737347811; p2=p1+t1{Cos[q1],Sin[q1]}; q2=2\[Pi]-q1; NSolve[p2[[2]]+t Sin[q2]\[Equal]1,t] Out[183]= {{t\[Rule]2.3094}} In[202]:= t2=2.3094010767585043; p3=p2+t2{Cos[q2],Sin[q2]}; q3=2\[Pi]-q2; NSolve[(p3[[1]]+t Cos[q3]+1)^2+(p3[]+t Sin[q3])^2==1,t] Out[205]= {{t\[Rule]0.200212},{t\[Rule]2.19472}} In[405]:= t3=2.194718395858327; p4=p3+t3{Cos[q3],Sin[q3]}; Solve[Ang[p4,p3,{-1,0}]\[Equal]Ang[p4,({Cos[t],Sin[t]}+p4),{-1,0}],t] From In[405]:= \!\(\* RowBox[{\(Power::"infy"\), \(\(:\)\(\ \)\), "\<\"Infinite expression \ \\!\\(1\\/0\\^2\\) encountered. \\!\\(\\*ButtonBox[\\\"More\[Ellipsis]\\\", \ ButtonStyle->\\\"RefGuideLinkText\\\", ButtonFrame->None, \ ButtonData:>\\\"Power::infy\\\"]\\)\"\>"}]\) From In[405]:= \!\(\* RowBox[{\(Solve::"ifun"\), \(\(:\)\(\ \)\), "\<\"Inverse functions are \ being used by \\!\\(Solve\\), so some solutions may not be found; use Reduce \ for complete solution information. \ \\!\\(\\*ButtonBox[\\\"More\[Ellipsis]\\\", ButtonStyle->\\\"RefGuideLinkText\ \\\", ButtonFrame->None, ButtonData:>\\\"Solve::ifun\\\"]\\)\"\>"}]\) Out[407]= {{t\[Rule]1.0472},{t\[Rule]1.19548}} In[328]:= q4=1.1954752520981573; NSolve[p4[[2]]+t Sin[q4]\[Equal]1,t] Out[329]= {{t\[Rule]2.04289}} In[440]:= t4=2.0428873267106815`; p5=p4+t4{Cos[q4],Sin[q4]}; q5=2\[Pi]-q4; 2 nd trajectory In[384]:= P0={0,0}; Q0=\[Pi]/9+\[Pi]/180; In[386]:= NSolve[(P0[[1]]+t Cos[Q0]-1)^2+(P0[[2]]+t Sin[Q0])^2==1,t] Out[386]= {{t\[Rule]0.},{t\[Rule]1.86716}} In[387]:= T0=1.8671608529944035`; P1=P0+T0{Cos[Q0],Sin[Q0]}; Q1=-\[Pi]+(ArcCos[P1[[1]]-1]+Q0); NSolve[P1[[2]]+t Sin[Q1]\[Equal]-1,t] Out[390]= {{t\[Rule]1.87331}} In[391]:= T1=1.8733090735550966`; P2=P1+T1{Cos[Q1],Sin[Q1]}; Q2=2\[Pi]-Q1; NSolve[P2[[2]]+t Sin[Q2]\[Equal]1,t] Out[394]= {{t\[Rule]2.24465}} In[395]:= T2=2.2446524752687225`; P3=P2+T2{Cos[Q2],Sin[Q2]}; Q3=2\[Pi]-Q2; NSolve[(P3[[1]]+t Cos[Q3]+1)^2+(P3[]+t Sin[Q3])^2==1,t] Out[398]= {{t\[Rule]0.341712},{t\[Rule]2.23354}} In[419]:= T3=2.233539454680641`; P4=P3+T3{Cos[Q3],Sin[Q3]}; Solve[Ang[P4,P3,{-1,0}]\[Equal]Ang[P4,({Cos[t],Sin[t]}+P4),{-1,0}],t] From In[419]:= \!\(\* RowBox[{\(Power::"infy"\), \(\(:\)\(\ \)\), "\<\"Infinite expression \ \\!\\(1\\/0\\^2\\) encountered. \\!\\(\\*ButtonBox[\\\"More\[Ellipsis]\\\", \ ButtonStyle->\\\"RefGuideLinkText\\\", ButtonFrame->None, \ ButtonData:>\\\"Power::infy\\\"]\\)\"\>"}]\) From In[419]:= \!\(\* RowBox[{\(Solve::"ifun"\), \(\(:\)\(\ \)\), "\<\"Inverse functions are \ being used by \\!\\(Solve\\), so some solutions may not be found; use Reduce \ for complete solution information. \ \\!\\(\\*ButtonBox[\\\"More\[Ellipsis]\\\", ButtonStyle->\\\"RefGuideLinkText\ \\\", ButtonFrame->None, ButtonData:>\\\"Solve::ifun\\\"]\\)\"\>"}]\) Out[421]= {{t\[Rule]1.09956},{t\[Rule]1.76035}} In[423]:= Q4=1.786499618850784`; NSolve[(P4[[1]]+t Cos[Q4]+1)^2+(P4[]+t Sin[Q4])^2==1,t] Out[424]= \!\({{t \[Rule] \(-2.961831812996791`*^-16\)}, {t \[Rule] 1.874216860919306`}}\) In[428]:= T4=1.874216860919306`; P5=P4+T4{Cos[Q4],Sin[Q4]}; Solve[Ang[P5,P4,{-1,0}]\[Equal]Ang[P5,({Cos[t],Sin[t]}+P5),{-1,0}],t] From In[428]:= \!\(\* RowBox[{\(Power::"infy"\), \(\(:\)\(\ \)\), "\<\"Infinite expression \ \\!\\(1\\/0\\^2\\) encountered. \\!\\(\\*ButtonBox[\\\"More\[Ellipsis]\\\", \ ButtonStyle->\\\"RefGuideLinkText\\\", ButtonFrame->None, \ ButtonData:>\\\"Power::infy\\\"]\\)\"\>"}]\) From In[428]:= \!\(\* RowBox[{\(Solve::"ifun"\), \(\(:\)\(\ \)\), "\<\"Inverse functions are \ being used by \\!\\(Solve\\), so some solutions may not be found; use Reduce \ for complete solution information. \ \\!\\(\\*ButtonBox[\\\"More\[Ellipsis]\\\", ButtonStyle->\\\"RefGuideLinkText\ \\\", ButtonFrame->None, ButtonData:>\\\"Solve::ifun\\\"]\\)\"\>"}]\) Out[430]= {{t\[Rule]-1.35509},{t\[Rule]-0.642004}} In[432]:= Q5=-0.6420035368814776`; Illustration In[451]:= Show[Graphics[{ Thickness[.003], Line[{{-1,-1},{1,-1}}], Line[{{-1,1},{1,1}}], Circle[{1,0},1,{-\[Pi]/2,\[Pi]/2}], Circle[{-1,0},1,{\[Pi]/2,3\[Pi]/2}], RGBColor[254/256,194/256,0], Thickness[.0051],PointSize[.03], Line[{p0,p0+t0{Cos[q0],Sin[q0]}}], Line[{p1,p1+t1{Cos[q1],Sin[q1]}}], Line[{p2,p2+t2{Cos[q2],Sin[q2]}}], Line[{p3,p3+t3{Cos[q3],Sin[q3]}}], Line[{p4,p4+t4{Cos[q4],Sin[q4]}}], Line[{p5,p5+1.9{Cos[q5],Sin[q5]}}], Point[p5+1.9{Cos[q5],Sin[q5]}], RGBColor[188/256,30/256,71/256], Line[{P0,P0+T0{Cos[Q0],Sin[Q0]}}], Line[{P1,P1+T1{Cos[Q1],Sin[Q1]}}], Line[{P2,P2+T2{Cos[Q2],Sin[Q2]}}], Line[{P3,P3+T3{Cos[Q3],Sin[Q3]}}], Line[{P4,P4+T4{Cos[Q4],Sin[Q4]}}], Line[{P5,P5+1.9{Cos[Q5],Sin[Q5]}}], Point[P5+1.9{Cos[Q5],Sin[Q5]}] }],AspectRatio\[Rule]Automatic] |
| Date | |
| Source | Own work |
| Author | Jakob.scholbach |
 |
This image could be recreated using vector graphics as an SVG file. This has several advantages; see Commons:Media for cleanup for more information. If an SVG form of this image is already available, please upload it. After uploading an SVG, replace this template with {{ vector version available|new image name.svg}}. |
Licensing
|
File usage
The following pages on Schools Wikipedia link to this image (list may be incomplete):
What is Schools Wikipedia?
Through Schools Wikipedia, SOS Childrens Villages has brought learning to children around the world. In 133 nations around the world, SOS Children's Villages works to bring better education and healthcare to families in desperate need of support. Have you heard about child sponsorship? Visit our web site to find out.

