
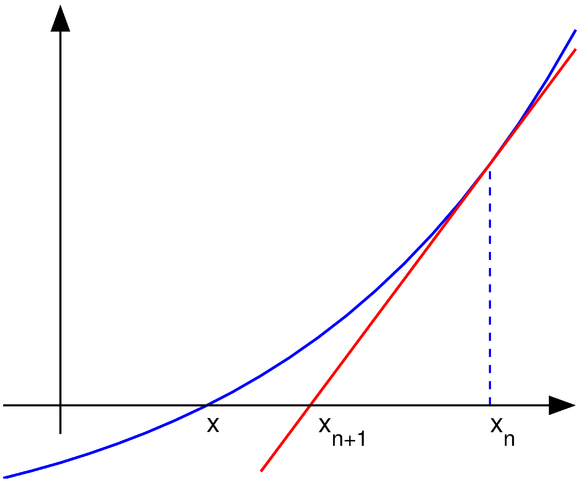
File:Newton iteration.png
Size of this preview: 583 × 479 pixels.
| |
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help. |
 |
File:Newton iteration.svg is a vector version of this file. It should be used in place of this raster image when superior. File:Newton iteration.png
For more information about vector graphics, read about Commons transition to SVG.
|
 |
| Description | Uploader graphed this with en:MATLAB (Illustration of en:Newton's method) |
| Date | 22 November 2004 (first version); 2004-11-23 (last version) |
| Source | Originally from en.wikipedia; description page is/was here. |
| Author | Original uploader was Olegalexandrov at en.wikipedia |
| Permission ( Reusing this file) |
Released into the public domain (by the author). |
|
|
This chart was created with MATLAB. |
Licensing
| Public domainPublic domainfalsefalse |
 |
This work has been released into the public domain by its author, Olegalexandrov at the English Wikipedia project. This applies worldwide. In case this is not legally possible: |
Source code ( MATLAB)
% illustration of Newton's method for finding a zero of a function function main () a=-1; b=1; % interval endpoints fs=20; % text font size % arrows settings thickness1=2; thickness2=1.5; arrowsize=0.1; arrow_type=1; angle=20; % in degrees h=0.1; % grid size X=a:h:b; % points on the x axis f=inline('exp(x)/1.5-0.5'); % function to plot g=inline('exp(x)/1.5'); % derivative of f x0=0.7; y0=f(x0); % point at which to draw the tangent line m=g(x0); Y=f(X); % points on the function to plot XT=-0.1:h:b; YT=y0+(XT-x0)*m; % tangent line % prepare the screen clf; hold on; axis equal; axis off % plot the graph and the tangent lines plot(X, Y, 'linewidth', thickness1) plot(XT, YT, 'r', 'linewidth', thickness1) plot([x0 x0], [0, y0], '--', 'linewidth', thickness2) % axes small=0.2; arrow([a 0], [b, 0], thickness2, arrowsize, angle, arrow_type, [0, 0, 0]) arrow([a+small, -0.1], [a+small, 1.4], thickness2, arrowsize, angle, arrow_type, [0, 0, 0]) % text H=text(-0.29, -0.06, 'x'); set(H, 'fontsize', fs) H=text(0.1, -0.1, 'x_{n+1}'); set(H, 'fontsize', fs) H=text(0.7, -0.1, 'x_{n}'); set(H, 'fontsize', fs) % save to disk saveas(gcf, 'newton_iteration.eps', 'psc2') function arrow(start, stop, thickness, arrow_size, sharpness, arrow_type, colour) % Function arguments: % start, stop: start and end coordinates of arrow, vectors of size 2 % thickness: thickness of arrow stick % arrow_size: the size of the two sides of the angle in this picture -> % sharpness: angle between the arrow stick and arrow side, in degrees % arrow_type: 1 for filled arrow, otherwise the arrow will be just two segments % color: arrow colour, a vector of length three with values in [0, 1] % convert to complex numbers i=sqrt(-1); start=start(1)+i*start(2); stop=stop(1)+i*stop(2); rotate_angle=exp(i*pi*sharpness/180); % points making up the arrow tip (besides the "stop" point) point1 = stop - (arrow_size*rotate_angle)*(stop-start)/abs(stop-start); point2 = stop - (arrow_size/rotate_angle)*(stop-start)/abs(stop-start); if arrow_type==1 % filled arrow % plot the stick, but not till the end, looks bad t=0.5*arrow_size*cos(pi*sharpness/180)/abs(stop-start); stop1=t*start+(1-t)*stop; plot(real([start, stop1]), imag([start, stop1]), 'LineWidth', thickness, 'Colour', colour); % fill the arrow H=fill(real([stop, point1, point2]), imag([stop, point1, point2]), colour); set(H, 'EdgeColor', 'none') else % two-segment arrow plot(real([start, stop]), imag([start, stop]), 'LineWidth', thickness, 'Colour', colour); plot(real([stop, point1]), imag([stop, point1]), 'LineWidth', thickness, 'Colour', colour); plot(real([stop, point2]), imag([stop, point2]), 'LineWidth', thickness, 'Colour', colour); end
File usage
The following pages on Schools Wikipedia link to this image (list may be incomplete):
More information
Wikipedia for Schools is one of SOS Childrens Villages' many educational projects. SOS Childrens Villages helps more than 2 million people across 133 countries around the world. Help another child by taking out a sponsorship.
