
File:Standard deviation.svg
- File
- File usage
- Metadata
- Background information
| |
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help. |
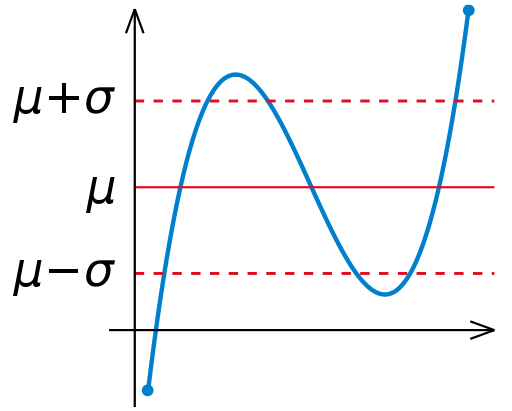
| Description | Illustration of en:Standard deviation |
| Date | 04:55, 4 August 2007 (UTC) |
| Source | self-made with MATLAB. Tweaked in Inkscape |
| Author | Oleg Alexandrov 04:55, 4 August 2007 (UTC) |
| Permission ( Reusing this file) |
PD-self |
| Public domainPublic domainfalsefalse |
 |
I, the copyright holder of this work, release this work into the public domain. This applies worldwide. In some countries this may not be legally possible; if so: I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law. Public domainPublic domainfalsefalse |
Source code ( MATLAB)
% Illustartion of standard deviation function main() a=-1.2; b = 1.3; c = -0.5; d = 2.5; N=100; X=linspace(a, b, N); Y=X.^3-0.2*X.^2-X+2; % Y=X.^2; % scale Y to fit in the plotting window Y = (Y-min(Y))/(max(Y)-min(Y)); Y = Y*(d-c)+c; mean = sum(Y)/length(Y); stdev = sqrt(sum((Y-mean).*(Y-mean))/length(Y)); figure(1); clf; hold on; axis off; axis equal; lw = 3; % linewidth lw2 = lw/2; lw3 = lw/1.5; fs = 30; % font size red=[0.867 0.06 0.14]; blue = [0, 129, 205]/256; green = [0, 200, 70]/256; black = [0, 0, 0]; % plot the curves shiftl=a-0.1; small=0.2; plot(X, Y, 'linewidth', lw, 'colour', blue); plot([shiftl max(X)+small], [mean, mean], 'linewidth', lw2, 'colour', red); plot([shiftl max(X)+small], [mean, mean]+stdev, 'linewidth', lw3, 'colour', red, 'linestyle', '--'); plot([shiftl max(X)+small], [mean, mean]-stdev, 'linewidth', lw3, 'colour', red, 'linestyle', '--'); % plot some balls for beauty n = length(X); ball_rad = 0.03; ball(X(1), Y(1), ball_rad, blue) ball(X(n), Y(n), ball_rad, blue) % axes small=0.2; arrowsize=0.2; arrow_type=0; angle=20; % in degrees arrow([shiftl-0.2 0], [b+0.2, 0], lw2, arrowsize, angle, arrow_type, black) arrow([shiftl, min(Y-0.1)], [shiftl, max(Y)], lw2, arrowsize, angle, arrow_type, black) % text small1 = 0.3; small2 = 0.3; text(shiftl-small1, mean, '\mu', 'fontsize', fs) text(shiftl-small1-small2, mean+stdev, '\mu+\sigma', 'fontsize', fs) text(shiftl-small1-small2, mean-stdev, '\mu-\sigma', 'fontsize', fs) % H=text(0.1, -0.1, 'x_{n+1}'); set(H, 'fontsize', fs) % H=text(0.7, -0.1, 'x_{n}'); set(H, 'fontsize', fs) % save to disk saveas(gcf, 'Standard_deviation.eps', 'psc2') % plot2svg('Standard_deviation.svg'); function arrow(start, stop, thickness, arrow_size, sharpness, arrow_type, colour) % Function arguments: % start, stop: start and end coordinates of arrow, vectors of size 2 % thickness: thickness of arrow stick % arrow_size: the size of the two sides of the angle in this picture -> % sharpness: angle between the arrow stick and arrow side, in degrees % arrow_type: 1 for filled arrow, otherwise the arrow will be just two segments % color: arrow colour, a vector of length three with values in [0, 1] % convert to complex numbers i=sqrt(-1); start=start(1)+i*start(2); stop=stop(1)+i*stop(2); rotate_angle=exp(i*pi*sharpness/180); % points making up the arrow tip (besides the "stop" point) point1 = stop - (arrow_size*rotate_angle)*(stop-start)/abs(stop-start); point2 = stop - (arrow_size/rotate_angle)*(stop-start)/abs(stop-start); if arrow_type==1 % filled arrow % plot the stick, but not till the end, looks bad t=0.5*arrow_size*cos(pi*sharpness/180)/abs(stop-start); stop1=t*start+(1-t)*stop; plot(real([start, stop1]), imag([start, stop1]), 'LineWidth', thickness, 'Colour', colour); % fill the arrow H=fill(real([stop, point1, point2]), imag([stop, point1, point2]), colour); set(H, 'EdgeColor', 'none') else % two-segment arrow plot(real([start, stop]), imag([start, stop]), 'LineWidth', thickness, 'Colour', colour); plot(real([stop, point1]), imag([stop, point1]), 'LineWidth', thickness, 'Colour', colour); plot(real([stop, point2]), imag([stop, point2]), 'LineWidth', thickness, 'Colour', colour); end function ball(x, y, r, colour) Theta=0:0.1:2*pi; X=r*cos(Theta)+x; Y=r*sin(Theta)+y; H=fill(X, Y, colour); set(H, 'EdgeColor', 'none');
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it. If the file has been modified from its original state, some details may not fully reflect the modified file.
Background information
SOS Children chose the best bits of Wikipedia to help you learn. Thanks to SOS Childrens Villages, 62,000 children are enjoying a happy childhood, with a healthy, prosperous future ahead of them. Sponsoring a child is a great way to help children who need your support.
