Khan Academy on a Stick
Limits
Limit introduction, squeeze theorem, and epsilon-delta definition of limits
-
 Introduction to limits
Introduction to limits
Introduction to limits
-
 Inferring limit from numerical data
Inferring limit from numerical data
-
 Estimating limit numerically
Estimating limit numerically
Limits
Limits are the core tool that we build upon for calculus. Many times, a function can be undefined at a point, but we can think about what the function "approaches" as it gets closer and closer to that point (this is the "limit"). Other times, the function may be defined at a point, but it may approach a different limit. There are many, many times where the function value is the same as the limit at a point. Either way, this is a powerful tool as we start thinking about slope of a tangent line to a curve. If you have a decent background in algebra (graphing and functions in particular), you'll hopefully enjoy this tutorial!
Estimating limits from graphs
In this tutorial, we will build our ability to visualize limits by estimating them based on graphs of functions. We will look at both one-sided and two-sided limits.
Finding limits algebraically
We often attempt to find the limit at a point where the function itself is not defined. In this tutorial, we will use algebra to "simplify" functions into ones where it is defined. Given that the original function and the simplified one may be identical except for the limit point in question, this is a useful way of finding limits.
Continuity using limits
A function isn't continuous when there is a "break" in its graph. This tutorial uses limits to define this idea more formally and gives practice thinking about continuity (and discontinuity) in terms of limits.
-
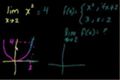 Introduction to limits
Introduction to limits
Introduction to the intuition behind limits
-
 Limit examples (part 1)
Limit examples (part 1)
Some limit exercises
-
 Limit examples (part 2)
Limit examples (part 2)
More limit examples
-
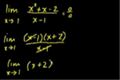 Limit examples (part 3)
Limit examples (part 3)
More limit examples
-
 Limit examples w/ brain malfunction on first prob (part 4)
Limit examples w/ brain malfunction on first prob (part 4)
3 interesting limit examples (correct answer for problem 1 is 3/16 (6/(4*8) NOT 6/(4+8))
-
 More limits
More limits
More limit examples
Old limits tutorial
This tutorial covers much of the same material as the "Limits" tutorial, but does it with Sal's original "old school" videos. The sound, resolution or handwriting isn't as good, but some people find them more charming.
Limits and infinity
You have a basic understanding of what a limit is. Now, in this tutorial, we can explore situation where we take the limit as x approaches negative or positive infinity (and situations where the limit itself could be unbounded).
-
 Squeeze theorem or sandwich theorem
Squeeze theorem or sandwich theorem
-
 Squeeze theorem exercise example
Squeeze theorem exercise example
-
 Squeeze theorem (sandwich theorem)
Squeeze theorem (sandwich theorem)
Intuition (but not a proof) of the Squeeze Theorem.
-
 Proof: lim (sin x)/x
Proof: lim (sin x)/x
Using the squeeze theorem to prove that the limit as x approaches 0 of (sin x)/x =1
Squeeze theorem
If a function is always smaller than one function and always greater than another (i.e. it is always between them), then if the upper and lower function converge to a limit at a point, then so does the one in between. Not only is this useful for proving certain tricky limits (we use it to prove lim (x → 0) of (sin x)/x, but it is a useful metaphor to use in life (seriously). :) This tutorial is useful but optional. It is covered in most calculus courses, but it is not necessary to progress on to the "Introduction to derivatives" tutorial.
-
 Limit intuition review
Limit intuition review
-
 Building the idea of epsilon-delta definition
Building the idea of epsilon-delta definition
-
 Epsilon-delta definition of limits
Epsilon-delta definition of limits
-
 Proving a limit using epsilon-delta definition
Proving a limit using epsilon-delta definition
-
 Epsilon-delta limit definition 1
Epsilon-delta limit definition 1
Introduction to the Epsilon Delta Definition of a Limit.
-
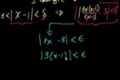 Epsilon-delta limit definition 2
Epsilon-delta limit definition 2
Using the epsilon delta definition to prove a limit
Epsilon delta definition of limits
This tutorial introduces a "formal" definition of limits. So put on your ball gown and/or tuxedo to party with Mr. Epsilon Delta (no, this is not referring to a fraternity). This tends to be covered early in a traditional calculus class (right after basic limits), but we have mixed feelings about that. It is cool and rigorous, but also very "mathy" (as most rigorous things are). Don't fret if you have trouble with it the first time. If you have a basic conceptual understanding of what limits are (from the "Limits" tutorial), you're ready to start thinking about taking derivatives.
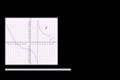 One-sided limits from graphs
One-sided limits from graphs Limit at a point of discontinuity
Limit at a point of discontinuity Determining which limit statements are true
Determining which limit statements are true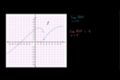 Two-sided limit from graph
Two-sided limit from graph Limit example 1
Limit example 1 Limit properties
Limit properties Limit by factoring cubic expression
Limit by factoring cubic expression Limits to define continuity
Limits to define continuity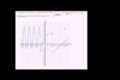 Limit and function defined at point of discontinuity
Limit and function defined at point of discontinuity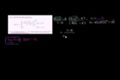 Fancy algebra to find a limit and make a function continuous
Fancy algebra to find a limit and make a function continuous Defining a function at a point to make it continuous
Defining a function at a point to make it continuous Limits and infinity
Limits and infinity Vertical asymptote of natural log
Vertical asymptote of natural log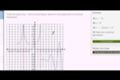 Visually determining vertical asymptotes
Visually determining vertical asymptotes Limits at positive and negative infinity
Limits at positive and negative infinity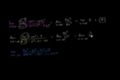 More limits at infinity
More limits at infinity Limits with two horizontal asymptotes
Limits with two horizontal asymptotes Limits at infinity using algebra
Limits at infinity using algebra