Khan Academy on a Stick
Derivative applications
Minima, maxima, and critical points. Rates of change. Optimization. L'Hopital's rule. Mean value theorem.
Equations of normal and tangent lines
A derivative at a point in a curve can be viewed as the slope of the line tangent to that curve at that point. Given this, the natural next question is what the equation of that tangent line is. In this tutorial, we'll not only find equations of tangent lines, but normal ones as well!
Motion along a line
Derivatives can be used to calculate instantaneous rates of change. The rate of change of position with respect to time is velocity and the rate of change of velocity with respect to time is acceleration. Using these ideas, we'll be able to analyze one-dimensional particle movement given position as a function of time.
Critical points and graphing with calculus
Can calculus be used to figure out when a function takes on a local or global maximum value? Absolutely. Not only that, but derivatives and second derivatives can also help us understand the shape of the function (whether they are concave upward or downward). If you have a basic conceptual understanding of derivatives, then you can start applying that knowledge here to identify critical points, extrema, inflections points and even to graph functions.
-
 Concavity, concave upwards and concave downwards intervals
Concavity, concave upwards and concave downwards intervals
-
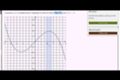 Recognizing concavity exercise
Recognizing concavity exercise
-
 Inflection points
Inflection points
-
 Graphing using derivatives
Graphing using derivatives
Graphing functions using derivatives.
-
 Another example graphing with derivatives
Another example graphing with derivatives
Using the first and second derivatives to identify critical points and inflection points and to graph the function.
Concavity and inflection points
Applying differentiation in different fields
The idea of a derivative being the instantaneous rate of change is useful when studying or thinking about phenomena in a whole range of fields. In this tutorial, we begin to just scratch the surface as we apply derivatives in fields as disperse as biology and economics.
Related rates
Have you ever wondered how fast the area of a ripple of a pond is increasing based on how fast the ripple is? What about how fast a volcano's volume is increasing? This tutorial on related rates will satiate your curiosity and then some! Solving related rates problems using calculus
-
 Mean value theorem
Mean value theorem
-
 Finding where the derivative is equal to the average change
Finding where the derivative is equal to the average change
-
 Getting a ticket because of the mean value theorem
Getting a ticket because of the mean value theorem
-
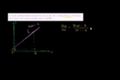 Maximizing function at value
Maximizing function at value
-
 Mean value theorem
Mean value theorem
Intuition behind the Mean Value Theorem
Mean value theorem
If over the last hour on the highway, you averaged 60 miles per hour, then you must have been going exactly 60 miles per hour at some point. This is the gist of the mean value theorem (which generalizes the idea for any continuous, differentiable function).
-
 Introduction to l'Hôpital's rule
Introduction to l'Hôpital's rule
Introduction to L'Hôpital's Rule
-
 L'Hôpital's rule example 1
L'Hôpital's rule example 1
L'Hôpital's Rule Example 1
-
 L'Hôpital's rule example 2
L'Hôpital's rule example 2
L'Hôpital's Rule Example 2
-
 L'Hôpital's rule example 3
L'Hôpital's rule example 3
L'Hôpital's Rule Example 3
-
 L'Hopital's Rule to solve for variable
L'Hopital's Rule to solve for variable
-
 Tricky L'Hopital's Rule problem
Tricky L'Hopital's Rule problem
-
 Proof of special case of l'Hôpital's rule
Proof of special case of l'Hôpital's rule
L'Hôpital's rule
Limits have done their part helping to find derivatives. Now, under the guidance of l'Hôpital's rule, derivatives are looking to show their gratitude by helping to find limits. Ever try to evaluate a function at a point and get 0/0 or infinity/infinity? Well, that's a big clue that l'Hopital's rule can help you find the limit of the function at that point.
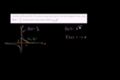 y-intercept of tangent line example
y-intercept of tangent line example Equation of normal line
Equation of normal line Equation of tangent line example 1
Equation of tangent line example 1 Total distance traveled by a particle
Total distance traveled by a particle Analyzing particle movement based on graphs
Analyzing particle movement based on graphs When is a particle speeding up
When is a particle speeding up Minima, maxima and critical points
Minima, maxima and critical points Finding critical numbers
Finding critical numbers Testing critical points for local extrema
Testing critical points for local extrema Identifying minima and maxima for x^3 - 12x + 2
Identifying minima and maxima for x^3 - 12x + 2 Extreme value theorem
Extreme value theorem Relative minima and maxima
Relative minima and maxima Identifying relative minimum and maximum values
Identifying relative minimum and maximum values Applying extreme value theorem
Applying extreme value theorem Minimizing sum of squares
Minimizing sum of squares Optimizing box volume graphically
Optimizing box volume graphically Optimizing box volume analytically
Optimizing box volume analytically Optimizing profit at a shoe factory
Optimizing profit at a shoe factory Minimizing the cost of a storage container
Minimizing the cost of a storage container Expression for combined area of triangle and square
Expression for combined area of triangle and square Minimizing combined area
Minimizing combined area Derivative and marginal cost
Derivative and marginal cost Approximating incremental cost with derivative
Approximating incremental cost with derivative Modeling a forgetting curve
Modeling a forgetting curve Rates of change between radius and area of circle
Rates of change between radius and area of circle Rate of change of balloon height
Rate of change of balloon height Related rates of water pouring into cone
Related rates of water pouring into cone Falling ladder related rates
Falling ladder related rates Rate of change of distance between approaching cars
Rate of change of distance between approaching cars Speed of shadow of diving bird
Speed of shadow of diving bird Local linearization
Local linearization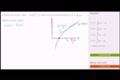 Local linearization example
Local linearization example