Rachel
About

Khan Academy on a Stick

Algebra basics

Negative numbers

Understanding and operating with negative numbers is key in algebra. This tutorial will make sure that you have the basics down!

  • Introduction to exponents

    Taking an exponent is basically the act of repeated multiplication. You know how to multiply, right? If so, understanding exponents is completely within your grasp!

  • Exponent example 1

  • Exponent example 2

  • Raising a number to the 0 and 1st power

    The progression of powers from zero to any non-zero number follows a pattern and can be logically explained. After watching this, it will make sense why any non-zero number to the zero power equals one.

  • Powers of 1 and 0

    Let's see what happens with bases to the zero power, plus we'll reinforce the patterns of applying exponents to postive and negative bases.

  • Powers of fractions

    Just like whole numbers with exponents, fractions are repeatedly multiplied. If you know how to multiply factions, you're over half way there.

  • Powers of zero

    We know that any non-zero number to the zero power equals one. We also know that zero to any non-zero exponent equals one. What happens when you have zero to the zero power?

The world of exponents

Addition was nice. Multiplication was cooler. In the mood for a new operation that grows numbers even faster? Ever felt like expressing repeated multiplication with less writing? Ever wanted to describe how most things in the universe grow and shrink? Well, exponents are your answer! This tutorial covers everything from basic exponents to negative and fractional ones. It assumes you remember your multiplication, negative numbers and fractions.

The square root

A strong contender for coolest symbol in mathematics is the radical. What is it? How does it relate to exponents? How is the square root different than the cube root? How can I simplify, multiply and add these things? This tutorial assumes you know the basics of exponents and exponent properties and takes you through the radical world for radicals (and gives you some good practice along the way)!

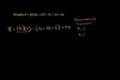Order of operations

If you have the expression "3 + 4 x 5", do you add the 3 to the 4 first or multiply the 4 and 5 first? To clear up confusion here, the math world has defined which operation should get priority over others. This is super important. You won't really be able to do any involved math if you don't get this clear. But don't worry, this tutorial has your back.

Fractions

This tutorial will help to review arithmetic with fractions

  • Fraction to decimal with rounding

    Sometimes when you convert a fraction to a decimal you have to do some long division and rounding.

  • Fraction to decimal

    Converting fractions to decimals sometimes requires us to brush up on our long division skills. We'll walk you through it.

  • Converting decimals to fractions example 3

    Converting this decimal results in a fraction that needs to be simplified. Can you help us?

  • Converting decimals to fractions 2 (ex 1)

  • Finding a percentage

    Once again, fractions are our friends as we use them to find a percentage. You'll also see a couple of different ways to arrive at the answer.

  • Percent word problem

    It's nice to practice conversion problems, but how about applying our new knowledge of percentages to a real life problem like recycling? Hint: don't forget your long division!

  • Percentage of a whole number

    We hope you're beginning to see that there's more than one way to skin a cat. In other words, there are several different ways to solve problems involving percentages, decimals, and fractions. Watch as find the percentage of a whole number.

Decimals, fractions and percentages

Let's review how to convert between fractions, decimals and percentages

Scientific notation

Scientists and engineers often have to deal with super huge (like 6,000,000,000,000,000,000,000) and super small numbers (like 0.0000000000532) . How can they do this without tiring their hands out? How can they look at a number and understand how large or small it is without counting the digits? The answer is to use scientific notation. If you come to this tutorial with a basic understanding of positive and negative exponents, it should leave you with a new appreciation for representing really huge and really small numbers!

Computing with scientific notation

You already understand what scientific notation is. Now you'll actually use it to compute values and solve real-world problems.

Perimeter and area of triangles

You first learned about perimeter and area when you were in grade school. In this tutorial, we will revisit those ideas with a more mathy lens. We will use our prior knowledge of congruence to really start to prove some neat (and useful) results (including some that will be useful in our study of similarity).

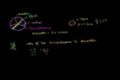  • Circles: radius, diameter, circumference and Pi

    A circle is at the foundation of geometry and how its parts relate to each other is both completely logical and a wonder.

  • Labeling parts of a circle

    Radius, diameter, center, and circumference--all are parts of a circle. Let's go through each and make sure we understand how they are defined.

  • Area of a circle

    In this example, we solve for the area of a circle when given the diameter. If you recall, the diameter is the length of a line that runs across the circle and through the center.

Circumference and area of circles

Circles are everywhere. How can we measure how big they are? Well, we could think about the distance around the circle (circumference). Another option would be to think about how much space it takes up on our paper (area). Have fun!