Khan Academy on a Stick
Graphs of trig functions
In this topic, we'll gain a deeper appreciation for the periodic nature of trig functions by visualizing and modeling real-world phenomena with them.
-
Midline, amplitude and period of a function
-
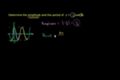Example: Amplitude and period
Determining the amplitude and period of a trig function
-
Example: Graph, domain, and range of sine function
Graphing a sin curve to think about its domain and range.
-
Example: Graph of cosine
Basic interpretation of the graph of the cosine function
-
Example: Intersection of sine and cosine
Thinking about where the graphs of sin and cos intersect.
-
Example: Amplitude and period transformations
Understanding how the amplitude and period changes as coefficients change.
-
Example: Amplitude and period cosine transformations
Visualizing changes in amplitude and period for a cosine function
-
Example: Figure out the trig function
Determining a trig function given its graph
-
Determining the equation of a trig function
-
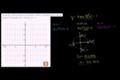Plotting maxima, minima and midline intersections of trig function
-
Tangent graph
Graphs of trig functions
The unit circle definition allows us to define sine and cosine over all real numbers. Doesn't that make you curious what the graphs might look like? Well this tutorial will scratch that itch (and maybe a few others). Have fun.
Modeling annual temperature variation with trigonometry
Applying inverse trig function with model
Modeling temperature through the day
Day length in AlaskaModeling with periodic functions
By now, you are reasonably familiar with the graphs of sine and cosine and are beginning to appreciate that they can be used to model periodic phenomena. In this tutorial, you'll get experience doing just that--modeling with periodic functions!
-
Tau versus pi
Why Tau might be a better number to look at than Pi
-
Pi is (still) wrong.
Please excuse the simple math and spelling errors. You shouldn't believe anything I say without double-checking even at the best of times. Go here: http://tauday.com/ and here: http://www.math.utah.edu/~palais/pi.html Me: http://vihart.com
Long live tau
Pi (3.14159...) seems to get all of the attention in mathematics. On some level this is warranted. The ratio of the circumference of a circle to the diameter. Seems pretty pure. But what about the ratio of the circumference to the radius (which is two times pi and referred to as "tau")? Now that you know a bit of trigonometry, you'll discover in videos made by Sal and Vi that "tau" may be much more deserving of the throne!