Matrices : Khan Academy on a Stick

Basic matrix operations

Keanu Reeves' virtual world in the The Matrix (I guess we can call all three movies "The Matrices") have more in common with this tutorial than you might suspect. Matrices are ways of organizing numbers. They are used extensively in computer graphics, simulations and information processing in general. The super-intelligent artificial intelligences that created The Matrix for Keanu must have used many matrices in the process. This tutorial introduces you to what a matrix is and how we define some basic operations on them.

Matrix multiplication

You know what a matrix is, how to add them and multiply them by a scalar. Now we'll define multiplying one matrix by another matrix. The process may seem bizarre at first (and maybe even a little longer than that), but there is a certain naturalness to the process. When you study more advanced linear algebra and computer science, it has tons of applications (computer graphics, simulations, etc.)

Properties of matrix multiplication

As we'll see, some of the properties of scalar multiplication (like the distributive and associative properties) have analogs in matrix multiplication while some don't (the commutative property).

Zero and identity matrices

In arithmetic, we learned than a number times 1 is still that number and that anything times 0 is 0. In this tutorial, we attempt to extend these ideas to the world of matrices!

Geometric transformations with matrices

We'll now see one of the most powerful applications of matrix multiplication--geometric transformations. This is core of what videos games and computer-based animation uses to "transform" figures based on movement or perspective. You probably never thought matrices could be so much fun!

Finding the determinant of a 2x2 matrix
Hint for finding the determinant of a 2x2 matrix
Inverse of a 2x2 matrix
Example of calculating the inverse of a 2x2 matrix
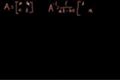Idea behind inverting a 2x2 matrix
What the inverse of a matrix is. Examples of inverting a 2x2 matrix.
Matrices to solve a system of equations
Using the inverse of a matrix to solve a system of equations.
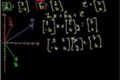Matrices to solve a vector combination problem
Using matrices to figure out if some combination of 2 vectors can create a 3rd vector
Finding the determinant of a 3x3 matrix method 1
Finding the determinant of a 3x3 matrix method 2
Inverting 3x3 part 1: Calculating matrix of minors and cofactor matrix
Beginning our quest to invert a 3x3 matrix. We calculate the matrix of minors and the cofactor matrix.
Inverting 3x3 part 2: Determinant and adjugate of a matrix
Finishing up our 3x3 matrix inversion
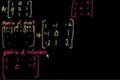Classic video on inverting a 3x3 matrix part 1
Inverting a 3x3 matrix
Classic video on inverting a 3x3 matrix part 2
Using Gauss-Jordan elimination to invert a 3x3 matrix.
Singular matrices
When and why you can't invert a matrix.

Inverting matrices

Multiplying by the inverse of a matrix is the closest thing we have to matrix division. Like multiplying a regular number by its reciprocal to get 1, multiplying a matrix by its inverse gives us the identity matrix (1 could be thought of as the "identity scalar"). This tutorial will walk you through this sometimes involved process which will become bizarrely fun once you get the hang of it.

Matrix equations

Matrices: Reduced row echelon form 1
Solving a system of linear equations by putting an augmented matrix into reduced row echelon form
Matrices: Reduced row echelon form 2
Another example of solving a system of linear equations by putting an augmented matrix into reduced row echelon form
Matrices: Reduced row echelon form 3
And another example of solving a system of linear equations by putting an augmented matrix into reduced row echelon form

Reduced row echelon form

You've probably already appreciated that there are many ways to solve a system of equations. Well, we'll introduce you to another one in this tutorial. Reduced row echelon form has us performing operations on matrices to get them in a form that helps us solve the system.